Dana jest funkcja angel754: Dana jest funkcja f(x)= −2 * (x−1)² + 3 a) Narysuj jej wykres. b) Podaj jej zbiór wartości oraz przedziały monotoniczności. c) Wyznacz najmniejszą i największą wartość tej funkcji w przedziale <1¹₂;10> d) Dla jakich wartości parametru m równanie |f(x)|−3= m ma dokładnie cztery rozwiązania?

angel754:

6latek: y=a(x−p)²+q jest to postac kanoniczna funkcji kwadratowej TY masz postac −2(x−1)¹+3 Co mozes z tej postaci odczytac ? A mozes dużo rzeczy odczytac .

6latek: poprawie ma być masz postac f(x)= −2(x−1)²+3

6latek: Przeciez jakies wiadomości musisz mieć (chodzisz przecież na lekcje

angel754: f(x)= −2(x−1)²+3 y= −2(x²−2*x*1+1²)+3 y=−2x²+4x−4+3 y=−2x²+4x−1 Δ=b² − 4ac Δ= 4²− 4* (−2) * (−1) Δ= 16 −8 Δ=8 √Δ = √8 p=^−b_2a q=^−Δ_4a p=⁻⁴₄=−1 q=⁻⁸₁₆= −¹₂ nie wiem czy dobrze zaczynam... i w sumie nie wiem tez co dalej

angel754: "jakieś wiadomości" mam ... ale nadrabiam dużą zaległość po chorobie i niestety nie umiem wszystkiego sobie sama wytłumaczyć. Chcę wrócić chociaż z nadrobionymi pracami domowymy, a pozniej bede prosila nauczycieli o poswiecenie mi chwili by wytłumaczyc funkcje. Tym bardziej ze z matmy jestem bardzo słaba. Mniejsza o to... dzięki za pomoc i jeśli mozesz mi cos jeszcze podpowiedziec bede wdzieczna.

6latek: No trochę nie Zobacz masz ta postac y=−2(x−1)²+3 To z tej postaci odczytujesz wspolrzedne wierzchołka paraboli czyli p=1 (lub inaczej x_w=1 i q=3 (lub inaczej y_w=3 Masz już jeden punkt do naszkicowania wykresu Ale z tej postaci również odczytujesz to ze a=−2 <0 i ramiona tej paraboli będą skierowane w dol czyli już nie musisz liczyc p i q ( co nawiasem mowiac policzylas zle Zajmujemy się teraz caly czas podpunktem a czyli do narysowania wykresu brakuje jeszcze miejsc zerowych i będziemy już mieli punkty szcegolne do narysowania wykresu To mamy y=−2(x−1)²+3 y= −2(x²−2x+1)+3 y=−2x²+4x−2+3 y=−2x²+4x+1 licz teraz x₁ i x₂

6latek: https://matematykaszkolna.pl/strona/69.html popatrz również tutaj

angel754: x1=^−4+√8₄= x2=

angel754: x1=^−4+√8₄=−1+√8 x2=^−4−√8₄= −1−√8 yyy chyba coś pokręciłam ?

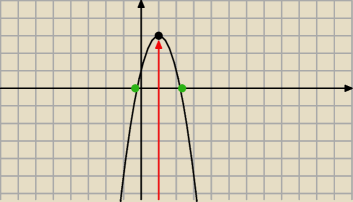
6latek: Tak teraz widać ze naprawdę masz kłopoty rachunkowe Δ=b²−4*a*c= 4²−4*(−2)*1=16+8=24 \ √24= √4*6= √4*√6= 2√6=√Δ

−b−√ Δ

−4−2√6

−4

2√6

√6

√6

x1=

=

=

−

= 1−

= 1+

2a

−4

−4

−4

−2

2

≈2,22

	−4+2√6		√6
x2= U{−b}+√Δ}{2a}=		= 1−		≈−0,22
	−4		2

Zobacz ze to się zgadza na rysunku Teraz zobacz ze fukcja ta rosnie dla x∊(−∞,1> a maleje x∊<1,∞) Zbior wartości odcztujesz po osi OY Z_wf= (−∞,3> Ogolnie jeśli a>0 to Z_wf= <q ,∞) jeśli a<0 to Z_wf = (−∞,q>

6latek:

6latek: Pocieszseniem dla Ciebie jest to ze nie tylko TY je masz ja również Przy obliczeniach korzystamy z takiej własności

a±b		a		b
	=		±
c		c		c

Przykład prosty

12+6		12		6
	=		+		+ 4+2=6
3		3		3

angel754: dzięki bardzo... ratujesz mi życie nigdy bym sama tego nie ogarnęła Czyli podpunkt a i od razu b mamy. A co z c i d? Podpowiesz jak to sprawdzić?

angel754: małe pocieszenie.... po Tobie nie widać zebyś miał problemy z matmą

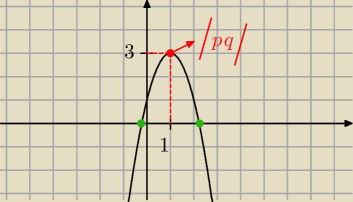
6latek: https://matematykaszkolna.pl/strona/3413.html Pomoge CI teraz ale naprawdę zapoznaj się z tym tutaj c) Mamy taki przedzial x∊<1,5,10 > Patrz teraz na wykres 11:46 Funkcja ta osiąga swoja najwieksza warosc dla x=1 i wynosi ona 3 . ALe nasze x=1 nie należy do tego przedzialu x∊(1,5,10> bo 1 nie należy d tego przedzialu Wiec będziemy musieli policzyć warosc tej funkcji dla x=1,5 i x=10 liczymy f(1,5)= −2(1,5)²+4*1,5 +1= −2*2,25+6+1= −4,5+6+1= 2,5 f(10)= −2*10²+4*10+1= −2*100+40+1= policz to Ta która jest mniejsza to wartość najmniejsza w tym przedziale a która wieksza to wartość najwiesza w tym przedziale

6latek: Bardzo się mylisz

6latek: Z tego najtrudniejszy to jest ostatni punkt

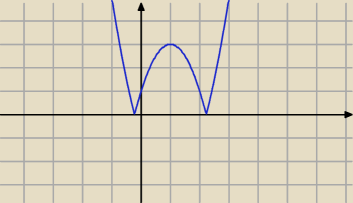
6latek: Należy zrobić następny wykres y=|f(x)|−3= y=|−2x²+4x+1| Z własności wartości bezwzględnej a mianowicie z tej ze jest ona zawsze nieujemna to co na wykresie y=−2x²+4x+1 jest pod osia OX musi powedrowac nad os OX TO będzie wykres f(x)= |−2x²+4x+1| Jeszcze musimy go obnizyc o 3 jednostki w dol bo mamy y= |−2x²+4x+1|−3 Narysuje go w następnym wpisie

angel754: Jeszcze raz dziękuje bardzo mi pomogłeś ! Głowa do góry i powodzenia obiecuje, że sie przyłożę !

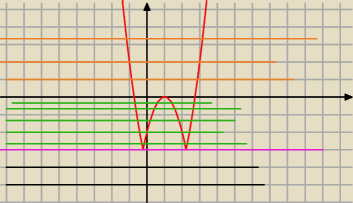
6latek: To jest wykres y=|f(x)|−3 teraz patrz dla y∊(−∞,−3) nie ma rozwiazan Prosta y=m nigdzie nie przecina tego wykresu dla y=−3 prosta ta przecina wykres w dwóch niejscach (mas dwa rozwiązania Teraz y∊(−3,0) prosta y=m przecina ten wykres w 4 miejscach (masz tutaj 4 rozwiązania Dla y=0 mmasz 3 rozwiązania dla y=(0,∞) masz 2 rozwiązania