wymierne (granice i inne 6latek : Wyznacz takie x₁<0 aby dla x<x₁ była spelniona nierownosc

	2
a) |		|<10−3
	1+x

2
	<10−3
1+x

2<10⁻³+10⁻³x −10⁻³x<10⁻³−2

	2
x>−1+
	10−3

x>−1+2*10³ x>2*10³−1 Natomiast w odpowiedzi mam x₁ = −2*10³−1

6latek : Gdzie ja robie blad przy oblczeniach

Jerzy: Cześć 1) Skąd masz trzecią linijkę ? 2) IaI < b ⇔ − b < a < b

6latek : czesc Jerzy

	2		2
Robilem tym sposobem zadania tutaj https://matematykaszkolna.pl/forum/326762.html Przyjalem ze 1+x>0 to |		|=		i
	1+x		x+1

pomnozylem obie strony nierownosci przez x+1

Jerzy: Na jakiej podstawie zakładasz,że : 1 + x > 0 ?

6latek : No bo ε promien otoczenia musi być dodatni

6latek : Te zadania sa oznaczone jako trudne wiec ja mogę się mylic . jeśli tak to powiedz proszse gdzie robie blad w mysleniu Wiem ze należy korzystać |m−a|<g

Jerzy: A skąd ja mam to wiedzieć ?

6latek : A czy to zalozenie 1+x>0 jest nieprawidłowe ?

Jerzy: skąd mam wiedzieć,że x = ε > 0 ?

6latek : J Ty wszystko wiesz

Jerzy: odnieś się do punktu 2)

6latek : Inaczej może Powiedz mi dlaczego w tamtych zadaniach takie rozwiązanie dzialao a w tym już nie działa ?

6latek : zaraz odpisze .

6latek : otoczeniem U(A,ε) o promieniu ε punktu A nazywamy odcinek otwarty tej prostej o srodku A i dlugosci 2ε Wiec jeśli punkt A ma wspolrzedna a to U(A,ε) jest (a−ε,a+ε) Teraz odniosie się do punktu 2 |x|<b to −b<x<b Wiec tak

2
	<10−3 to (wiesz co ? chyba nie mysle
x+1

Jerzy:

	2
− 10−3 <		< 10−3
	x+1

6latek :

	2		2
ja to bym rozbil na dwie nierownosci		<10−3 i		>−10−3
	x+1		x+1

I mam wlasnie kłopot z rozwiazniem tego Czy to mozyc przez kwadrat mianownika obie strony czy przenosić wszystko na lewo i przyrownac do zera i potem dostanie się nierownosc wielomianowa ?

6latek :

Jerzy:

	2
A jak byś liczył:		< 10
	x+1

6latek :

2
	−10<0
x+1

U{2}−10(x+1)}{x+1}<0

2−10x−10
	<0
x+1

−10x−8
	<0
x+1

(−10x−8)(x+1)<0 itd.

Jack: no to jest ok, co teraz napisales.

Jerzy: No to teraz zamast 10 , masz 10⁻³

Jack: jesli nie masz zalozen dotyczacych iksa to rozwiazujesz tak jak teraz, czyli post 17:45.

6latek : Myslalem ze się przespie to będzie lepiej Tutaj mogbym zapisac tak ewentualnie

2		1
	<
x+1		103

	2		1
teraz		−		<0
	x+1		103

	2*103−(x+1
Teraz		<0
	103(x+1)

2*103−x−1
	<0
103(x+1)

U{(−x+2*10³−1)(10³x+10³)<0 Tu już się pogubie w obliczeniach

6latek : Niech ktoś rozwiaze jedna z tych nierownosci

52: 6latku ale co tu się gubić ? x=2*10³ v x=−1 I rysujesz

52: x=2*10³−1 v x=−1

6latek : Czesc Po kiego grzyba ja się pchałem w dalsze wymnazanie tego jak ja mam tutaj postac iloczynowa Chyba pojde dalej

52: Hej, najpierw skończ Prześpij się, wróć do tego

6latek : czyli będzie x∊(−∞,−1)U(1999,∞)

52: mhh

Antek: Szukamy x1 ujemnego znacznie oddalonego od zera, więc x+1<0

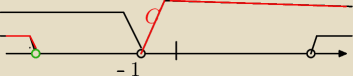
6latek : Teraz mamy druga nierownosc

2
	>−10−3
+1

	2		1
		>−
	x+1		103

2		1
	+		>0
x+1		103

2*103+x+1
	>0
103(x+1

(x+(2¹0³+1))(10³x+10³)>0 x=−2*10³−1 lub x=−1 x∊(−∞,−2*10³−1)U(−1,∞) Teraz koniunkcja rozwiazan x=−2*10³−1 =============

Antek: Możemy pomnożyć przez mianownik i zmienić zwrot nierówności

6latek : Antek . To jeśli szukamy x₁ ujemnego czy x+1<0 to x<−1 czy możemy w takim razie zapisac tak

	2
|		|<10−3 dla x<−1 |x+1|= −(x+1)= −x−1
	x+1

2
	<10−3 i to rozwiazac ?
−x−1

czy lepiej jest korzystać z własności wartości bezwzgledenej |x|<a −a<x<a ? i rozwiazywac dwie nierownosci ?

Antek: Korzystanie z własności wartości bezwzględnej jest uniwersalnym sposobem.... nie ma jednej recepty na te przyklady, choć w tych zadaniach chodzi raczej o szacowania i korzystanie z początkowych założeń

6latek : Dzieki

6latek : No bo jesli moge tak zapisac jak post 18:54 to mam wtedy lzejszse obliczenia

2
	<10−3
−x−1

2<10⁻³(−x−1) 2<−x*10⁻³−10⁻³ x*10⁻³<−2−10³ x<−2*10³−1

Mila: x<0

	2
−10−3<		<10−3
	x+1

	2		2
⇔		>−10−3 i		<103 i x<0 /*(x+1)
	x+1		x+1

1) x∊(−1,0)⇔x+1>0 2>−10⁻³*(x+1) i 2<10⁻³*(x+1)⇔ −10⁻³*x−10⁻³ <2 i 10⁻³*x+10⁻³>2 −10⁻³*x <2+10⁻³ i 10⁻³*x>2−10⁻³⇔ x>−2*10³−1 i x>2*10³ −1 i x<0 brak rozwiązań w przedziale (−1,0) 2) x<−1

2		2
	>−10−3 i		<103 i x<−1 /*(x+1)
x+1		x+1

x+1<0 2<−10⁻³*(x+1) i 2>10⁻³*(x+1)⇔ −10⁻³*x−10⁻³ >2 i 10⁻³*x+10⁻³<2 −10⁻³*x>10⁻³ +2 i 10⁻³*x<−10⁻³+2 x<−2*10³−1 i x<2*10³ −1 i x<−1 x<−2*10³−1

6latek : Dziekuje CI bardzo

6latek : Ten przyklad bedzie podobny

	4x−1
|		−4|<10−8
	x−3

Natomiast mam trzeci jeszcze do tego zadania

	6x2−1
|		−3|<0,01
	2x2+1

Robie to tak

	3(2x2+1)−4
|		−3|<0,01
	2x2+1

	−4
|		|<0,01 dla 2x2+1>0 zawsze
	2x2+1

Teraz mam pytanie Muszse rozwiazac dwie nierownosci

	−4
1)		<10−2
	2x2+1

2) U{−4}{2x²+1>−10⁻² ?

6latek : Poprawie druga

−4
	>−10−2
2x2+1

Mila: To którą rozwiązać i jakie są założenia?

6latek : Milu Takie same zalozenia jak w pierwszej i trzecia

6latek : Miałem się Ciebie pytac w osobnym poscie ale skro już jesteś to zapytam do 1 nierownosci My rozpatrujemy tutaj dwa przedzialy 1. x∊−1,0) 2 x∊(−∞,−1)

	2		|2|		2
dlatego ze Mamy mieć x<0 i |		|=		=
	x+1		|x+1|		|x+1|

Teraz x+1=0 to x=−1 czyli z wartości bezzglednej z mianownika mamy 2 przedzialy te które napisalas Tak ?

Mila:

	4x−1
|		−4|<10−8 tę?
	x−3

6latek : Milu z ta sobie poradzę

	6x2−1
ta |		−3|<0,01
	2x2+1

Mila: 21:39 Tak. Dla x∊(−1,0) mamy x+1>0 Dla x<−1 mamy x+1<0 i przy mnożeniu obu stron nierówności w tym przypadku zmieniamy kierunek nierówności.

6latek : To dobrze rozumiem Nie mam się kogo zapytać dlatego pytam Ciebie tutaj

Mila:

	6x2−1
|		−3|<0.01
	2x2+1

	6x2−1
−0.01<		−3<0.01 /*(2x2+1)
	2x2+1

−0.01*(2x²+1)<6x²−1−3*(2x²+1)<0.01*(2x²+1)⇔ 6x²−1−6x²−3>−0.01*(2x²+1) i 6x²−1−6x²−3<0.01*(2x²+1) −4>−0.01*(2x²+1) /*(−100) i −4<0.01*(2x²+1) /*100 2x²+1>400 i 2x²+1>−400 2x²−399>0 i 2x²+401>0 spełnione dla każdego x∊R

	399
x2−		>0 i x∊R
	2

	√399		√399
x<−		lub x>
	√2		√2

6latek : Dziekuje CI na razie

Mila:

Mila: Masz problemy to pytaj, gdy widzę, że masz pomoc, to nie wtrącam się, aby nie siać zamętu w komentarzach.

6latek : Czasmi sa problemy natury rachunkowej jak np. tutaj Ja wtedy potrzebuje jak to mowia gotowca gdyż nie pojde do szkoły i nie zapytam się nauczyciela Czasami wpadne po podpowiedzi na rozwiązanie ale czasami nie . A nie ma się kogo zapytać

6latek : Ale dobrze ze pomagasz

6latek : Ogarnalem ten trzeci przyklad

	399
x1= −√		to jst rozwiazanie
	2