zef i algebra liniowa Mariusz: Chciałbym abyś poćwiczył tutaj podstawy algebry liniowej Zagadnienia algebry liniowej które przydają się przy całkowaniu Dodawanie i odejmowanie wielomianów Mnożenie wielomianów Dzielenie wielomianów z resztą Schemat Hornera Rozkład wielomianu na czynniki nierozkładalne nad R NWD wielomianów (wykorzystując rozkład na czynniki oraz biorąc kolejne reszty) Rozkład na sumę ułamków prostych (wystarczy przypadek pierwiastków pojedynczych) Rozwiązywanie układów równań liniowych Tutaj proponuję metody macierzowe Ax=B A⁻¹Ax=A⁻¹B Ix=A⁻¹B x=A⁻¹B Inny sposób LU=PA Ax=B PAx=PB LUx=PB L⁻¹LUx=L⁻¹PB Ux=L⁻¹PB Niech L⁻¹PB=y wówczas otrzymamy L⁻¹PB=y Ux=y LL⁻¹PB=Ly Ux=y PB=Ly Ux=y Ostatecznie otrzymujemy Ly=PB Ux=y Zarówno do odwracania macierzy jak i do rozkładu LU proponuję użyć operacji elementarnych na wierszach Operacje elementarne 1. Dodanie wybranego wiersza pomnożonego przez skalar do innego wiersza 2. Pomnożenie wybranego wiersza przez skalar różny od zera 3. Zamiana dwóch wybranych wierszy (wykonanie tej operacji powoduje konieczność wprowadzenia macierzy permutacji w rozkładzie LU wykonujmy je więc w sytuacji gdy pojawi się zero na głównej przekątnej)

zef: Postaram się to poczytać w ciągu tygodnia, jak będę miał czas, w najbliższe dni rozwiąże również tą całkę którą mi podałeś i postaram się poprawić błędy w rozkładzie na ułamki proste.

Mariusz: http://matwbn-old.icm.edu.pl/kstresc.php?tom=11&wyd=10&jez=pl Ściągnij sobie ten pdf Przeczytaj sobie rozdział o macierzach , rozwiązywaniu równań liniowych i wielomianach

zef: Poczytałem trochę na ten temat, ale póki co chyba nie jest mi to potrzebne Muszę poszukać kogoś kto mnie dobrze przygotuje do matury, a całkami będę zajmował się rzadziej. Chcę zrobić cały materiał z 3 klasy zaczynając od teraz i kończąc we wrześniu Muszę jeszcze kogoś chętnego znaleźć do przerabiania materiałów ze mną po kolei.

Mariusz: Dodawanie i mnożenie wielomianów przyda się podczas rozkładu funkcji wymiernej na sumę ułamków Dzielenie z resztą przydaje się gdy stopień wielomianu z licznika jest większy od stopnia wielomianu z mianownika oraz do policzenia NWD wielomianów Schemat Hornera do obliczania wartości wielomianu Mimo iż dwa pierwsze punkty schematu całkowania funkcji wymiernych nie wymagają rozkładu mianownika na czynniki nierozkładalne nad R to jednak trzeci punkt już go wymaga więc w pewnych przykładach rozkładu mianownika na czynniki nie unikniesz NWD wielomianów przydaje się do skracania licznika z mianownikiem oraz do wydzielenia części wymiernej całki (przydatne w przypadku pierwiastków wielokrotnych mianownika) NWD wielomianów możesz też wykorzystać do usunięcia pierwiastków wielokrotnych z rozwiązywanego równania Rozkład na sumę ułamków prostych Po podzieleniu licznika przez mianownik i wydzieleniu części wymiernej całki może zostać do scałkowania funkcja wymierna gdzie mianownik zawiera tylko pierwiastki pojedyncze Podczas wydzielania części wymiernej całki oraz podczas rozkładu na sumę ułamków będziesz porównywał wielomiany w liczniku i stąd dostaniesz układ równań liniowych który najlepiej rozwiązać z użyciem macierzy odwrotnej lub rozkładu macierzy (wystarczy LU ) Co masz na maturze bo ludzie pisali że dużo wycięli z programu

zef: Głównie mi zależy na: Trygonometria − tutaj umiem tylko podstawy podstaw, ze względu na to co miałem jedynie na podstawie. Pochodne−pochodne które są na poziomie licealnym umiem liczyć, ale zależy mi na zadaniach tekstowych. nie umiem wyznaczać pierwiastków wielomianu za pomocą pochodnych itd. Podsumowując umiem je tylko liczyć Wielomiany− tutaj już skończyliśmy przerabiać materiał i myślę że jestem dobrze przygotowany, chociaż zadania związane z resztą mogą mi sprawiać problemy. Na samym początku chciałbym zająć się tymi trzeba działami, później będę mógł przejść do trudniejszych rzeczy.

zef: Znalazłbyś trochę czasu i chęci aby odłożyć na tą chwilę całki i zająć się moim przygotowaniem do matury ? Potrzebowałbym jakieś zadania i pewnie dużo twojej pomocy.

Mariusz: Chcesz kilka zadań ze zbioru Dróbki i Szymańskiego ?

zef: Przyda mi się wszystko co masz.

Mariusz: Jeśli chodzi o stronę z odnośnika to analizę miałeś w tomie 15 http://matwbn-old.icm.edu.pl/kstresc.php?tom=15&wyd=10&jez=pl Co do zadań z Dróbki Szymańskiego to np W trójkącie równoramiennym ABC (AC=BC) z wierzchołka C poprowadzono 2 półproste dzielące kąt ACB na 3 przystające kąty Półproste te przecinają podstawę AB w punktach D i E tak że D leży między A i E

	AD
Wyznacz stosunek		mając dany kąt ACB=3α
	DE

W kwadracie ABCD punkt E jest środkiem boku CD Proste BE i AC przecinają się w punkcie F Wykaż że tg ECF=1, tg CEF=2, tg EFC=3 Może zadania z trygonometrii przeniesiemy do innego wątku ?

6latek : czy zadania z geometrii pochodzą ze zbioru zadań z geometrii dla klasy 1 i 2 liceum ogolnoksztalcacego(1998r ?

Mariusz: Rok się zgadza ale dla klasy 3 i 4

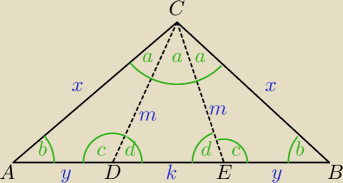
yht: Zadanie z trójkątem:

AD		y
	= ? →		= ?
DE		k

wszystkie kąty: a,b,c,d uzależniamy od a: c+d = 180⁰ → d=180⁰−c w ΔACE: b+d+2a = 180⁰ b+180⁰−c + 2a = 180⁰ b−c+2a = 0 b = c−2a w ΔACD: a+b+c = 180⁰ a+c−2a+c = 180⁰ 2c−a = 180⁰ 2c = 180⁰+a

	a
c = 900 +
	2

b=c−2a

	a
b=900+		−2a
	2

	3
b=900−		a
	2

d=180⁰−c

	a
d=1800−(900+		)
	2

	a
d=900−
	2

z tw. sinusów w ΔADC

x		y
	=
a   sin(900+ )   2		sin(a)

	y*sin(900+a2)
x =		− równanie (*)
	sin(a)

z tw. sinusów w ΔACE

x		y+k
	=
a   sin(900− )   2		sin(2a)

	(y+k)*sin(900−a2)
x =		− równanie (**)
	sin(2a)

Porównując równania (*) i (**) otrzymujemy:

y*sin(900+a2)		(y+k)*sin(900−a2)
	=		− równanie (***)
sin(a)		sin(2a)

ze wzorów redukcyjnych:

	a		a
sin(900+		) = cos(		)
	2		2

	a		a
sin(900−		) = cos(		)
	2		2

ze wzoru na sinus podwojonego kąta: sin(2a) = 2sin(a)*cos(a) wstawiając to do równania (***) otrzymujemy:

a   y*cos( )   2		a   (y+k)*cos( )   2
	=
sin(a)		2sin(a)*cos(a)

	sin(a)
Mnożymy stronami przez
	a   cos( )   2

	y+k
y =
	2cos(a)

	y
Przekształcamy tak aby otrzymać szukany iloraz		:
	k

	y+k
y =		|*2cos(a)
	2cos(a)

y*2cos(a) = y+k y*2cos(a)−y = k y[2cos(a)−1] = k

y[2cos(a)−1]
	= 1
k

y		1
	=
k		2cos(a)−1

AD		1
	=
DE		2cos(a)−1

	AD
Koniec zadania. Uzależniliśmy iloraz		od (danego w zadaniu) kąta a
	DE

*** zadanie z kwadratem: niech: kąt ECF = α kąt CEF = β kąt EFC = γ z sumy kątów w trójkącie EFC wiadomo, że γ = 180⁰−(α+β) α to kąt między przekątną kwadratu a jego bokiem, więc α = 45⁰ więc tgα = 1 tgβ łatwo wyznaczyć z trójkąta prostokątnego BEC mając tgα oraz tgβ korzystamy ze wzoru redukcyjnego na tgγ tgγ = tg[180⁰−(α+β)] = −tg(α+β) wykorzystujemy wzór na tg(α+β) i wychodzi

zef: Tak, zacznijmy trygonometrię w tym temacie 326264