Trygonometria zef: Trygonometria

Iryt: I co?

zef: Nic, będę tu ćwiczył trygonometrię z pomocą Mariusza

Mila: Powodzenia

Mariusz: W trójkącie prostokątnym ABC z wierzchołka C poprowadzono dwusieczną CD

	DB
Oblicz stosunek długości boków		gdy
	BC

I BC=x AC=a II BC=x AB=a III AC=x AC=a Milu jak chcesz możesz się dołączyć Coś rysunki mi tutaj nie wychodzą Zadanie może nie jest wyszukane bo sam je wymyślałem ale z pewnością przyda ci się w przyszłości

zef: Dzisiaj chyba czasu nie znajdę na zrobienie tego zadania bo na jutro mam dużo do zrobienia. Chociaż jeszcze zobaczę.

Mariusz: poprawka III AC=x AB=a

zef: Wierzchołek C jest przy kącie prostym ?

Mariusz: Przy wierzchołku B jest kąt prosty

zef:

db
	=?
bc

db		db
	=
bc		x

	x
tg2β=
	a

x		2tgβ
	=
a		1−tg2β

	a(2tgβ)
x=
	1−tg2β

z=

	z
tgα=
	x

z=x(tgβ)

z		x(tgβ)
	=
x		a(2tgβ)   1−tg2β

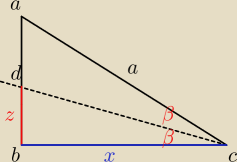
z		1−tg2β
	=x(tgβ)*
x		a(2tgβ)

z		1−tg2β
	=x(tgβ)*
x		2a(tgβ)

z		x(1−tg2β)
	=
x		2a

O to chodzi ? Nie miałem jeszcze wzorów na tg2α itd więc musiałem poszukać wzorku w internecie.

zef: Aj źle jest już widzę błąd. Zrobię jeszcze raz.

Mila: zef, tw. o dwusiecznej kąta w trójkącie.

zef: Rysunek ten sam:

db
	=?
bc

|da|		|ac|
	=
|db|		|bc|

	ad
tgβ=
	ac

ac(tgβ)=ad

ac(tgβ)		|ac|
	=
|db|		|bc|

	|ac|*|db|
|ac|(tgβ)=
	|bc|

	db
tgβ=
	bc

Zgadza się teraz?

zef: Hmm w sumie nic nie wykazałem Nie wiem jak się za to zabrać.

Mariusz:

	BD
W 1 przypadku masz wyrazić stosunek		za pomocą
	BC

BC=x, AC=a

	BD
W 2 przypadku masz wyrazić stosunek		za pomocą
	BC

BC=x , AB=a

	BD
W 3 przypadku masz wyrazić stosunek		za pomocą
	BC

AC=x, AB=a Wierzchołki powinieneś oznaczyć dużymi literami aby nie myliło się z długością boku

zef: Spróbuję jeszcze jutro na spokojnie to zrobić, bo teraz już nie myślę

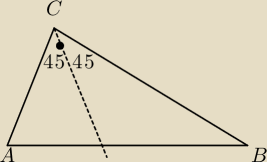
Jack: nie jest powiedziane, przy ktorym wierzcholku jest kat prosty.

Mariusz: Mila załóżmy że tego twierdzenia nie znamy , znamy twierdzenie sinusów , twierdzenie cosinusów (tutaj wystarczy Pitagorasa) itp zef miałeś twierdzenie o dwusiecznej na lekcji ?

zef: Niestety nie miałem

Mariusz: Jack gdybyś czytał wszystkie posty to byś wiedział że przy B jest kąt prosty na początku nie dopisałem bo nie sądziłem że to jest istotne ale zef mnie zapytał przy jakim wierzchołku jest kąt prosty to mu napisałem Przy danych jakie podałem kątem prostym jest ten przy wierzchołku B Kąta prostego nie dzielimy bo nie uzyskamy tego co bym chciał abyśmy uzyskali Masz rację że powinienem od razu zaznaczyć kąt prosty

Mariusz: zef więc nie powinieneś z niego korzystać Twierdzenie sinusów miałeś ? Możesz zastąpić twierdzenie o dwusiecznej twierdzeniem sinusów

Mila: To w której klasie jesteś zef?

zef: Twierdzenie sinusów również nie.. Wspominałem już że trygonometrię miałem tylko na podstawie. Miałem tyle co w pierwszej klasie. Teraz jestem w drugiej

Jack: twierdzenie sinusów i cosinusów jest bardzo proste, radze sie zapoznac(programowo jest w trzeciej klasie) jednak wiele zadan mozna obliczyc korzystajac wlasnie z tych twierdzen nawet wczesniej.

zef: Twierdzenie cosinusów już znam, chociaż nie musiałem, ale przydawało mi się w planimetrii

Jack: sinusow jest prostsze i je sie poznaje przed cosinusami ; d

Mila: Twierdzenie o dwusiecznej też powinieneś znać. Było już w gimnazjum. Tw. cosinusów, tw. sinusów jest w I klasie, albo w drugiej, zależy jakim programem się uczycie, jakiego autora masz podręcznik, może mam, to dostosuję zadania.

Mariusz: Jak twierdzenia sinusów nie miałeś to bieda chociaż może jeszcze da radę jakoś inaczej Może coś z polem Ja jeszcze miałem twierdzenie sinusów , nie pamiętam abym miał twierdzenie o dwusiecznej Stosunek z twierdzenia o dwusiecznej będzie przydatny jednak ty musisz do tego jakoś inaczej dojść Znasz program trzeciej klasy ?

Jack: Milu ja tw. cos. i sin. mialem w 3 klasie a matma byla rozszerzona... ciekawe ; d

zef: Dobra możemy uznać że te twierdzenia znam, przecież nie są one trudne

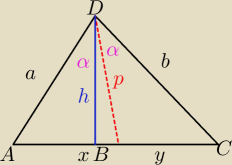
Jack: Niech dwusieczna nazywa sie "p" a wysokosc trojkata "h". Korzystamy ze wzoru na pole trojkata wykorzystujac kat. (1/2 ab sin alfa) zatem :

	1		PABD
PABD =		* a * p * sin −−>> p sinα =
	2		a

	1		PBCD
PBCD =		* b * p * sin α −−−> p sin α =
	2		b

przyrownujemy do siebie...

PABD		PBCD
	=
a		b

b * P_ABD = a * P_BCD

	1
Pole trojkata ABD mozna zapisac rowniez jako		* x* h
	2

	1
a pole trojakta BCD mozna zapisac jako		* y * h
	2

zatem mamy

	1		1
b *		* x* h = a *		* y * h
	2		2

zatem bx = ay czyli

a		b
	=
x		y

i to mowi tw. o dwusiecznej.

Mariusz:

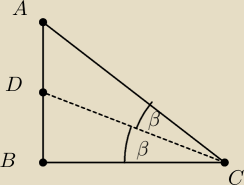
	DB
Obliczyć		gdy dane mamy
	BC

I BC=x AC=a II BC=x AB=a III AC=x AB=a Sami widzicie że rysowanie mi nie wychodzi

Mariusz:

	BC
Pytanie dodatkowe czy rozpoznajecie stosunek
	DB

Mariusz: W przypadku I sprawdź czy długość boków BC, AB wyrażają się wymiernie przez znaleziony stosunek i długość boku AC W przypadku II sprawdź czy długość boków BC, AC wyrażają się wymiernie przez znaleziony stosunek i długość boku AB W przypadku III sprawdź czy długość boków AC, BC wyrażają się wymiernie przez znaleziony stosunek i długość boku AB Jeśli to sprawdzisz będziesz miał pewność że to zadanie ci się kiedyś przyda

6latek : mam taki zbior dla klasy 3 i 4 liceum ale z 1973r . Nie wiesz czy się zmienily zadania w stoeuku do 1998r ?

6latek : Albo jeśli możesz to napisz który dzial i nr zadania masz u siebie w zbiorze to porównam u siebie

6latek : mam ten tylko ze z 1973r http://allegro.pl/zbior-zadan-z-matematyki-drobka-szymanski-i5114072664.html

Mariusz: 6latek to zadanie z dwusiecznymi kątów ostrych w trójkącie prostokątnym przyda mu się do wymyślania podstawień usuwających niewymierność czy to z równania czy to z całki Ja mam zbiór zadań z I i II klasy (rok 1996) oraz z III i IV klasy (rok 1998) bo wtedy chodziłem do liceum Razem możemy porównać zadania

Mariusz: W Tym zbiorze nie ma jednak ciekawych zadań a jeśli chodzi o tw sinusów i cosinusów to ty ich na razie nie znasz 4.10. W trójkącie równoramiennym dane są długość podstawy 10 cm i kąt przy podstawie równy 30° Oblicz długość promienia koła wpisanego w trójkąt i opisanego na trójkącie 130 W trójkącie równoramiennym kąt przy podstawie jest α a przy wierzchołku jest β

	15
Mając dane sin(α)=		, oblicz sin(β) i cos(β)
	17

ale dokończ to zadanie z dwusiecznymi bo bardziej ci się przyda W trójkącie ABC poprowadzono dwusieczne kątów ostrych CD i AE

	BE		AB		DB		BC
Wyraź stosunki		,		,		,
	AB		BE		BC		DB

przez dwa wybrane boki trójkąta ABC

	3 2
Możliwości wyboru dwóch boków trójkąta jest

czyli tyle ile nam potrzeba bo tyle jest przypadków postaci kanonicznej trójmianu kwadratowego

6latek : Piszac Zbior zadań z geometrii dla klasy 1 i 2 liceum ogolnoksztalcacego miałem na myśli ten zbior http://allegro.pl/zbior-zadan-z-geometrii-kl-i-ii-drobka-szymanski-i5711951117.html

zef: Nie mogę ostatnio znaleźć jakoś chwili na rozwiązanie tego, powinienem zrobić to w tym tyogdniu.

Mariusz: zef twoje podejście do mojego zadania też było dobre tylko źle zidentyfikowałeś tg2β (zły stosunek boków z nim skojarzyłeś) Twoje podejście powinno doprowadzić do równania kwadratowego Wzoru na tg2β nie miałeś ? Mimo to dobrze go napisałeś

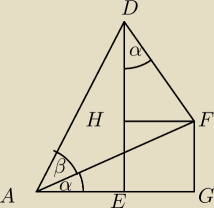
Mariusz: Wyprowadź wzór na funkcje trygonometryczne sumy