zadanie GIGANT: Witam, Mam pytanie, na jakiej podstawie w I sposobie otrzymaliśmy, że sin(180* − α − β ) = sin( α + β ) .... ? http://www.zadania.info/d89/4730671 Jakoś tego nie kapuje. Nawet gdybyśmy znali alfe i bete to nie może się równać... Dla przykładu α = 30, β = 40 sin(180 − 30 − 40 ) = sin(110*) i to ma się równać sin( 30 + 40 ) = sin70? Chociaż teraz jak to napisałem to przypomniało mi się, że istnieje coś takiego jak okresowość funkcji i to, że daną wartość otrzymuje dla różnych miar kątów. Chociaż dla sinusa jest to co 2π więc jakoś mi nie pasuje...W każdym razie prosiłbym o pomoc dlaczego tak, a nie inaczej Pozdrawiam

#62;#62;: sin(180−30−40) = sin[180−(30+40)] = sin(180−70) = sin70

Janek191: Mamy wzór redukcyjny : sin ( 180^o − α) = sin α W tym przypadku sin ( 180⁰ − α − β) = sin ( 180^o − ( α + β)) = sin ( α + β)

GIGANT: Taki bajer Raczej bym na to nie wpadł. Cóż człowiek uczy sie całe życie, dzięki wielkie

6latek : Dlatego ze sin(180−α−β)=sin(180−(a+β) Teraz jest ważne (α+β)=δ traktujemy jako jeden kat (oznaczyłem go tak żeby nie mieszac Ze wzoru redukcyjnego mamy sin(180^o−δ)=sinδ ====================== Ale nasz e δ= (α+β) wiec sin(180^o−(α+β)= sin(α+β) Mysle ze to będzie jasne

6latek : Janek191 już CI rozpisal tez

GIGANT: Tak, tak dzięki... Po prostu zabrakło mi na tamtej stronie, że sin( 180* − ( alfa + beta ) ) dzięki

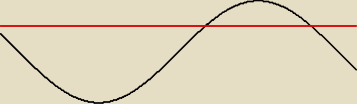
Przemysław: Czerwona prosta jest na wysokości wartości 1/2 Widać, że nawet w jednym okresie sinus przyjmuje wartość 1/2 dla dwóch różnych argumentów ta górka jest w 90^o i to się zgadza z Twoim przykładem: 90−70=110−70=20 odległości od górki są takie same. sin(180^o−(α+β))=sin(α+β) oznaczę a=α+β, żeby nie przepisywać wystarczy by było: sin(180^o−a)=sin(a) Z wzoru na sinusa różnicy kątów: sin(180^o−a)=sin180^ocos(−a)+sin(−a)cos180^o sin180^o=0 cos180^o=−1 sin180^ocos(−a)+sin(−a)cos180^o=0−sin(−a) ale wiemy, że: sin(−a)=−sin(a), czyli: 0−sin(−a)=−(−sin(a))=sin(a) Tutaj masz dowód na sinus sumy: http://www.math.us.edu.pl/~pgladki/faq/node98.html A tutaj trochę wzorków: http://www.matemaks.pl/wzory-trygonometryczne.html https://matematykaszkolna.pl/strona/450.html

Przemysław: Widzę, że wszyscy się rzuciliśmy