objętość czworościanu - matura maturalna: Dwie przeciwległe , nawzajem skośne krawędzie czworościanu mają tę samą długość a, są wzajemnie prostopadłe i prostopadłe do odcinka o długości b, łączącego ich środki. Oblicz objętość tego czworościanu.

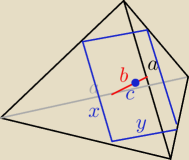
g: Prostokąt o bokach x, y wynika z przecięcia czworościanu płaszczyzną prostopadłą do odcinka b przecinającą b w odległości c od jego końca. x = a*(c/b) y = a*((b−c)/b)

	a2
V = ∫0b x*y dc =		∫0b c*(b−c) dc
	b2

∫ c*(b−c) dc = b*c²/2 − c³/3

	a2
V =		* (b3/2 − b3/3) = a2*b/6
	b2

maturalna: dzięki, spójrz tez na to https://matematykaszkolna.pl/forum/index.html