.. Radek: Wyznacz wszystkie wartości parametru a dla których równanie ma dokładnie dwa pierwistki 3x⁵ − 5x³ +a = 0 Nie bardzo wiem jak to zadanie ruszyć i prosze o pomoc z jakimś wyjaśnieniem jakby istniała taka możliwość

Metis: Czy równanie jest na pewno dobrze przepisane?

Radek: Tak, na pewno

Radek: Pierwsza myśl to coś z pochodnymi pokombinować, ale nie bardzo wiem co i jak

Jack: a = 5x³ − 3x⁵ = x³(5−3x²)

Radek: a coś więcej? Nie za wiele mi to niestety mówi

Jack: hm...chwilke, musialbym pomyslec ; D

ICSP: wielomian stopnia nieparzystego posiada nieparzystą liczbę pierwiastków.

Jack: ICSP, a to nie jest czasem "maxymalnie" ? wielomian stopnia drugiego posiada max 2 pierwiastki, zatem 5tego stopnia max 5

ICSP: Widziałeś kiedyś wielomian stopnia III który posiadał dwa pierwiastki ?

DziekujePanStanislaw: tak ja widzialem tylko ze jeden podwojny

DziekujePanStanislaw: np (x−1)²(x+1)

ICSP: Łącznie posiada 3. x = 1 , x = 1 , x = −1

Metis: (x−1)²(x+1)=0 3 pierwiastki 2 rozwiązania

DziekujePanStanislaw: ale jest jeden XDDD to sie nazywa jeden podwojny pierwiastek i jest traktowany jako jeden plcm przeczytac definicje pierwiastkow wielokrotnych

DziekujePanStanislaw: nope 2 pierwiastki z czego jeden jest dwukrotny

ICSP: Ech...

Jack: ja zawsze mowie ze rozwiazaniem rownania (x−2)² jest dwojka (jest pierwiastkiem podwojnym, ale jest jedenym rozwiazaniem) wiec rozwiazanie jest jedno...

Metis: 300298

Metis: Ja źle piszę (x−1)²(x+1)=0 Ma dwa pierwiastki w tym jeden podwójny

DziekujePanStanislaw: pomoze ktos w tym zadanku

Radek:

ICSP: Przecież macie już gotowy schemat postępowania

Radek: Nie czuje tego zadania

ICSP: PodWeźmy ich przykład : f(x) = (x−1)²(x+1) ma on dwa (trzy) rozwiązania. Pytanie: Dlaczego ?

Radek: Bo wielomian jest trzeciego stopnia?

mock: ponieważ, "zeruje się" dla 1,−1 ?

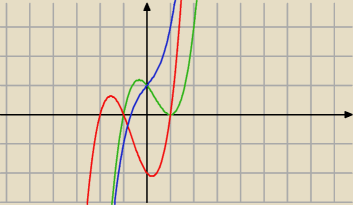
ICSP: Masz tu trzy przykłady wielomianów stopnia III. Tylko zielony posiada dwa różne pierwiastki. Zauważ, że w punkcie x = 1 odbija się on od osi odciętych, więc warunkiem wystarczającym na to aby wielomian stopnia III miał dwa różne pierwiastki jest posiadanie przez niego ekstremum znajdującego się na osi odciętych. Idee tą można bardzo łatwo przenieść na wielomian stopnia V.

Radek: Dziękuje za objaśnienie, spróbuje coś pokombinować, jak nie uda sie rozwiązac to się jeszcze zgłosze

mock: i jak Radek, ogarnales to zadanie? bo ja nie bardzo

mock: ktos jest w stanie?

Radek: ja nic nie wymyslilem

ICSP: Przelicze to ... f(x) = 3x5 − 5x3 +a f'(x) = 15x²(x² − 1) f'(x) = 0 ⇒ x = 0 v x = 1 v x = −1 Punkt x = 0 jest punktem przegięcia a w punktach x = 1 v x = −1 funkcja posiada ekstrema. Chcemy waby wartości ekstremów były równe 0 . f(1) = 3 − 5 + a = 0 ⇒ a = 2 f(−1) = −3 + 5 + a = 0 ⇒ a = −2 Odp a ∊ {−2 , 2}

Radek : Fajnie, ze ktoś sie pode mnie podszywa xd