W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość a. Kąt między
mock: W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość a. Kąt między krawędzią
boczną i podstawą jest równy kątowi płaskiemu przy wierzchołku ostrosłupa. Oblicz objętość
tego ostrosłupa.
26 kwi 17:26
mock: prosilbym o rozwiazanie, poniewaz nie potrafie tego zrobic
proboje to rozwiazac z 2. trojkatow(o tym samym kacie) ale nie potrafie dojść do postaci z
jedną zmienną

26 kwi 17:33
mock: jest ktos w stanie mi pomoc?
26 kwi 18:36
26 kwi 19:00
Mila:
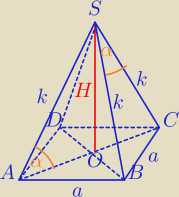
W ΔSOA:
H=0.5tgα*a
√2
| | 0.5a√2 | | a√2 | |
cosα= |
| ⇔k*cosα=0.5a√2⇔k= |
| ⇔ |
| | k | | 2cosα | |
WΔSBC:
a
2=k
2+k
2−2k
2*cosα
a
2=2k
2*(1−cosα)⇔
Z (1) i (2)
| a2 | | a2 | |
| = |
| oblicz z tego cosα, |
| 2*(1−cosα) | | 2cos2α | |
przy czym cosα>0 bo α jest kątem ostrym.
Próbuj dalej sam.
Będę później.
26 kwi 19:28
Mila:
Widzę, że czekasz na gotowca, za kilka dni znowu wpiszesz to zadanie?
cd.
1−cosα=cos
2α
cos
2α+cosα−1=0
Δ=5
| | −1−√5 | |
cosα= |
| <0 nie odpowiada założeniom, lub |
| | 2 | |
sin
2α+cos
2α=1
| | √5−1 | | √√5−1 | |
sin2α= |
| ⇔sinα= |
| |
| | 2 | | √2 | |
| | √√5−1 | | 2 | | √2 | |
tgα= |
| * |
| = |
| *√√5+1 |
| | √2 | | √5−1 | | 2 | |
H=0.5tgα*a
√2
=================
26 kwi 20:53
mock: Wow, dzięki

Nie czekałem na gotowca, poprostu robiłem kolejny arkusz i przez ~3h nie robiłem nic poza nim

26 kwi 23:20
Mila:
A masz chociaż odpowiedzi do tego zadania?
26 kwi 23:28
26 kwi 23:34
mock: przy jedynce trygonometrycznej jak sie nie myle, maly blad rachunkowy
26 kwi 23:35
mock: ale nie wiem gdzie

26 kwi 23:40
Mila:
E, dobrze obliczyłam. Trzecia od dołu dobrze, a potem...
Błędnie przepisałam H w dwóch ostatnich linijkach.
26 kwi 23:41
mock: a no faktycznie
26 kwi 23:44


 Nie czekałem na gotowca, poprostu robiłem kolejny arkusz i przez ~3h nie robiłem nic poza nim
Nie czekałem na gotowca, poprostu robiłem kolejny arkusz i przez ~3h nie robiłem nic poza nim

