Objętość ostrosłupa Rycerz: W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość a. Kąt między krawędzią boczną i podstawą jest równy kątowi płaskiemu przy wierzchołku ostrosłupa. Oblicz objętość tego ostrosłupa. Proszę o pomoc!

Rycerz: Pomocy błagam :')

Mila:

	1
V=		*a2*H
	3

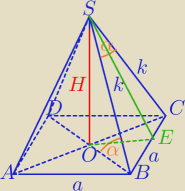
W ΔBES: a²=k²+k²−2*k*k*cosα a²=2k²−2k²*cosα

	a2
a2=2k2(1−cosα)⇔1−cosα=		⇔
	2k2

	a2
(1) 1−cosα=
	2k2

W ΔSOB:

	OB
cosα=		⇔
	k

	0.5a√2		a√2
cosα=		⇔cosα=		⇔
	k		k

	a2
(2) cos2α=
	2k2

Z (1 i 2) cos²α=1−cosα cos²α+cosα−1=0 i α − kąt ostry⇔cosα>0 Δ=1+4=5

	−1+√5
cosα=
	2

	0.5a√2		a√2		√5−1
cosα=		⇔		=		⇔
	k		2k		2

	a*(√10+√2
k=
	4

	a√2
k2=		)2+H2
	2

	a2*(√10+√2)2		a2
H2=		−
	16		2

	a2*[(√10+√2)2−8]
H2=
	16

Dokończ rachunki i podstaw do wzoru na V Jutro spojrzę.