..
Paweł:
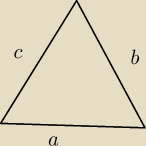
Mam takie pytanie, chce obliczyć objętość kuli wpisanej i opisanej na czworościanie foremnym.
Narysowałem przekrój czworościanu i nie wiem czy dobrze oznaczyłem boki. ''d'' to krawędź
czworościanu
c=d
25 kwi 19:18
Paweł: I jeśli to jest okej to potem standardowo okrąg wpisany i opisany na trójkącie ?
25 kwi 19:25
5-latek : Przeciez czworościan foremny slada się trojkatow równobocznych wiec ma wszystkie boki rowne
25 kwi 19:26
Paweł: No tak, ale przekrój też bedzie miał wszystkie boki równe?
25 kwi 19:29
Paweł: Wydaje mi sie że nie

25 kwi 19:30
Paweł: Ktoś rzuci okiem?
25 kwi 19:39
5-latek : narysuj sobie czworościan foremmy i spróbuj wpisac w niego kule
Albo to zrob sobie w jakims programie (teraz sa
Wiesz ze srodek okręgu wpisanego i opisanego w trojkacie równobocznym to te same punkty
Gdzie pada wysokość takiego czworościanu na podstawe ?
25 kwi 19:41
25 kwi 19:46
Paweł: 
25 kwi 19:55
Mila:
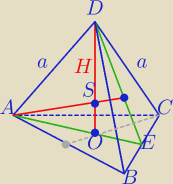
|OD|=H
H
2+|AO|
2=a
2
| | a√6 | |
r= |
| −promień kuli wpisanej |
| | 12 | |
| | a√6 | |
R= |
| − promień kuli opisanej |
| | 4 | |
25 kwi 20:06
Mila:
W czworościanie foremnym o krawędzi a:
r:R=1:3
25 kwi 20:08
25 kwi 20:09
Paweł: Dziękuje za takie szczegółowe wyjaśnienie

, a skąd wiadomo że OS = 1/4H?
25 kwi 20:11
Paweł: Troche sie już pogubiłem, to kule wpisaną w okrąg można przyjąć za okrąg wpisany w przekrój czy
nie?
25 kwi 20:15
Paweł: 
25 kwi 20:54
Mila:
Okrąg jest wpisany w "kawałek" przekroju. Znajdę rysunek to dam linka, albo narysuję.
Kula wpisana w czworościan jest styczna do jego ścian.
Punkt S jest jednakowo odległy od ścian ostrosłupa ( czworościanu).
S jest przecięciem wysokości czworościanu, które przecinają się w jednym punkcie
i dzielą w stosunku 1:3.
To możesz wykazać.
Półprosta ES jest dwusieczną ∡AED ⇒
=================
Wzór na promień kuli wpisanej w czworościan można inaczej wyprowadzić.
25 kwi 21:02
Paweł: Dziękuje Milu, znalazłem Twoje stare rysunki w innych tematach więc nie musisz rysować drugi
raz. Już rozumiem te kule i
czworościany. Jeszcze raz dziękuje

25 kwi 21:04
Metis: Masz gdzieś te linki ?

25 kwi 21:08
25 kwi 21:10
Metis: O super

Nie widziałem go wcześniej

25 kwi 21:11
Paweł: Też średnio rozumiesz te kule wpisane opisane czy tylko powtórka?
25 kwi 21:14
Metis: Powtórka i nie

25 kwi 21:15
Mila:
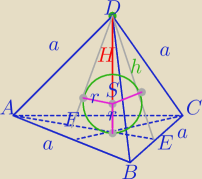
ABCD− czworościan foremny.
| | |FE|+2h | | 4 | | 4 | | a√3 | |
PΔFED= |
| *r= |
| h*r= |
| * |
| *r |
| | 2 | | 3 | | 3 | | 2 | |
stąd:
25 kwi 21:19
Paweł: To tak podsumowując, warto zapamiętać do matury że promień kuli wpisanej w czworościan to 1/4H
a opisanej to 3/4H gdzie
H to wysokość tego ''kawałka'' przekroju czyli trójkąta równoramiennego, tak?
25 kwi 21:23
Paweł: To teraz gdzieś jeszcze poszukam zadań z tymi kulami wpisanymi w bryły żeby to przećwiczyć.
Dziękuje Milu za super wyjaśnienie


25 kwi 21:25
Mila:
H− wysokość czworościanu foremnego!.
Tak, to należy zapamiętać, przydaje się.
25 kwi 21:26
Mila:
1) Zadanie dla maturzystów − kule wpisane i opisane na ostrosłupie.
Dany jest ostrosłup prawidłowy czworokątny, w którym kąt nachylenia ściany bocznej
| | π | |
do podstawy jest równy |
| . |
| | 3 | |
Wyznacz stosunek długości promienia kuli opisanej
do długości promienia kuli wpisanej w ten ostrosłup.
25 kwi 22:14
Paweł: Spróbuje rozwiązać

25 kwi 23:26
Metis: Rozwiązuj na kartce i podaj wynik!

25 kwi 23:28
Paweł: Wyszło mi 2, ale nie bardzo jestem pewny

25 kwi 23:35
Paweł: wycofuje
25 kwi 23:37
Paweł: przeczytałem krawędzi bocznej a w poleceniu jest ściany.. późna godzina daje o sobie troche
znac
25 kwi 23:37
Paweł: Tutaj też mi się nasuwa pytanie, jaka jest różnica między przekrojem zawierającym przekątną
podsstawy, a tą łączącą krawędzie boczne podstawy?
Czy w zależności od danych możemy którąś wybrać czy jest jakaś inna zależność? Stereometria to
moja pięta Achillesowa

25 kwi 23:43
Paweł: Metis potrafiłbyś to wytłumaczyć ?
25 kwi 23:51
25 kwi 23:52
Metis: Paweł sprecyzuj to pomożemy

25 kwi 23:56
Paweł: na kartce machne i wrzuce zdjęcie
25 kwi 23:59
Metis: Evelek masz


Ten kąt wiele ułatwia− mamy wtedy trójkąt równoboczny.
Można też wyjść ze wzoru r kuli wpisanej w dowolny wielościan wypukły:
| | 3V | |
r= |
| ( nie musimy interesować się zbytnio kątem) |
| | Pc | |
ale oczywiście do czasu, gdy trzeba będzie sparametryzować do jednej niewiadomej

O R kuli opisanej na ostrosłupie już łatwiej.
26 kwi 00:00
Evelek: 
26 kwi 00:06
Paweł: http://iv.pl/images/31629865538488465136.jpg wybacz, że tak niechlujnie, ale nie chce Ci zabierać czasu

.
Jest jakaś różnica w zastosowaniu któregoś przekroju? Pamiętam, że natrafiłem kiedyś na takie
zadanie, że TRZEBA było wykorzystać przekrój z przekątną.
26 kwi 00:06
Evelek: Maturka to będzie formalność haha.

26 kwi 00:07
Evelek: Pawel roznica istotna. Przekatna podstawy ma inna długość niż ten odcinek laczacy srodki
podstaw. Następną wazna rzecz: Kat miedzy sciana boczna a podstawa nie jest taki sam jak
miedzy krawędzią boczna a podstawa.
26 kwi 00:08
Metis: Paweł nie wiem o jakie zadanie chodziło, ale to po prostu dwa inne przekroje ostrosłupa.
26 kwi 00:09
Paweł: Tak straszyli rok temu maturą, a nie była wcale trudna to w tym mogą coś podrzucić

26 kwi 00:10
Metis: Precyzując, między płaszczyzną podstawy .
26 kwi 00:11
Paweł: Czyli przekrój ''wybieram'' w zależności od danych i w zależności od tego czego szukam tak?
26 kwi 00:11
Metis: No oczywiście, że tak.
26 kwi 00:11
Evelek: Wszystko zalezy od zadania. Polecenie w zadaniu ci mówi co masz zrobić. W tym zadaniu od Mila
mieliśmy wyznaczyć promienie R i r kul wpisanej i opisanej w ten ostrosłup. Wiec najszybsza
droga do tego to wykorzystanie przekroju który narysowalem w swoim rozwiązaniu, czyli odcinek
laczacy srodki boków podstawy.
Są zadania gdzie masz np. wyznaczyć sinus kąta miedzy krawędzią boczna ostroslupa a jego
podstawa. To wtedy aby wyznaczyć taki kat to bierzesz pod uwagę przekątna podstawy i krawędź
boczna, czyli ten ostroslup który narysowales i zaznaczyles w nim właśnie te odcinki.

26 kwi 00:12
Paweł: Dzięki Wam

, już wszystko powtórzone tylko z tą stereometrią walcze, ale mam jeszcze troche
czasu żeby ją podszkolić.
26 kwi 00:12
Evelek: Rozszerzenie tez zdajesz?

26 kwi 00:14
Paweł: Taak i właśnie tej stereometrii najbardziej się obawiam, o reszte jestem w miare spokojny
26 kwi 00:15
Mila:
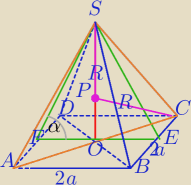
R− promień okręgu opisanego na ΔACS
r− promień okręgu wpisanego w ΔFES.
Liczcie.
26 kwi 00:20
Mila:
Ewelek popraw.
Dobranoc

26 kwi 00:21
Metis: Dobranoc
Milu 
26 kwi 00:22
Paweł: Dobranoc !
26 kwi 00:23
Paweł: Czyli rozwiązanie Ewelka jest złe?
26 kwi 00:25
Metis: Tak

26 kwi 00:25
Evelek: O kurczę taki błąd.. Widzę już, poprawie jutro w sql.

26 kwi 00:26
Paweł: a byś wyjaśnił co zrobiłeś źle?
26 kwi 00:27
Evelek: Dobra zrobię teraz i ci pokaze.
26 kwi 00:27
Paweł: Wielkie dzięki

26 kwi 00:29
Evelek: Generalnie jeden duży błąd. Kula opisana na ostroslupie. Promień tej kuli mieści sie w
przekroju ostroslupa który laczy przekatna podstawy i jego wierzchołek.
26 kwi 00:31
Paweł: Też tak na tym rysunkiem Mili posiedziałem i to ma sens. Dobra, lece spać bo już i tak myślenia
zbyt dużego teraz nie mam

26 kwi 00:34
26 kwi 01:05
26 kwi 01:05
Evelek: Idealnie w czasie.

26 kwi 01:05
Metis: Zdążyłeś ode mnie przepisać

26 kwi 01:06
Evelek: Haha innym sposobem zrobiłem.

26 kwi 01:07
Metis: Takie chciałbym na maturze

26 kwi 01:08
Evelek: Jakby takie na maturach były to by chyba wszyscy w tym kraju studiowali.

26 kwi 01:09
Paweł: Witam ponownie

, jak zawsze z pytaniami.. Na rysunku Mili widać że promień okregu OPISANEGO
idzie od punktu S
do punktu P to dlaczefo musimy skorzystać z przekroju zawierającego przekątna (pomaranczowy)?
Dlaczefo nie mozna wykorzystać tego zielonego?
Obliczajac PS zamiast PC?
26 kwi 10:00
Paweł: Dobra, już ogarnąłem temat.. udało mi się jakoś samemu

26 kwi 11:10
Evelek: Trzeba pamiętać który promień której kuli które odcinki łączy.

Tak btw, tu nie ma okręgów tylko kule w tym zadaniu.

Bo gdybyśmy chcieli opisać okrąg na tym
trójkącie to zrobiliśmy to tak jak ja na poczatku, wtedy stosunek wyniósłby 2.
26 kwi 12:01
Mila:
|AB|=2a
H=a
√3
| | a√3 | |
r= |
| − ΔFES− Δrównoboczny o boku (2a) |
| | 3 | |
R można obliczyć z tw. Pitagorasa w ΔPOC:
R
2=|OP|
2+|OC|
2
R
2=(H−R)
2+(a
√2)
2
2HR=H
2+2a
2
2*a
√3*R=(a
√3)
2+2a
2
2a*
√3*R=3a
2+2a
2
2
√3R=5a
26 kwi 15:09
Mila:
Tak zrobił
Metis, dopiero teraz zobaczyłam.

26 kwi 15:11
Metis: 
26 kwi 15:16
Mila:
Wzór na promień kuli wpisanej w ostrosłup podany przez
Metisa też warto zapamiętać.
V− objętość ostrosłupa
r− długość promienia kuli wpisanej w ostrosłup
P− pole powierzchni całkowitej ostrosłupa
===============================
26 kwi 15:21
 Mam takie pytanie, chce obliczyć objętość kuli wpisanej i opisanej na czworościanie foremnym.
Narysowałem przekrój czworościanu i nie wiem czy dobrze oznaczyłem boki. ''d'' to krawędź
czworościanu
Mam takie pytanie, chce obliczyć objętość kuli wpisanej i opisanej na czworościanie foremnym.
Narysowałem przekrój czworościanu i nie wiem czy dobrze oznaczyłem boki. ''d'' to krawędź
czworościanu


 |OD|=H
|OD|=H
 , a skąd wiadomo że OS = 1/4H?
, a skąd wiadomo że OS = 1/4H?




 Nie widziałem go wcześniej
Nie widziałem go wcześniej 

 ABCD− czworościan foremny.
ABCD− czworościan foremny.






 http://s31.postimg.org/q7lh3fyrf/WP_20160425_23_50_01_Pro.jpg
http://s31.postimg.org/q7lh3fyrf/WP_20160425_23_50_01_Pro.jpg


 Ten kąt wiele ułatwia− mamy wtedy trójkąt równoboczny.
Można też wyjść ze wzoru r kuli wpisanej w dowolny wielościan wypukły:
Ten kąt wiele ułatwia− mamy wtedy trójkąt równoboczny.
Można też wyjść ze wzoru r kuli wpisanej w dowolny wielościan wypukły:
 O R kuli opisanej na ostrosłupie już łatwiej.
O R kuli opisanej na ostrosłupie już łatwiej.

 .
Jest jakaś różnica w zastosowaniu któregoś przekroju? Pamiętam, że natrafiłem kiedyś na takie
zadanie, że TRZEBA było wykorzystać przekrój z przekątną.
.
Jest jakaś różnica w zastosowaniu któregoś przekroju? Pamiętam, że natrafiłem kiedyś na takie
zadanie, że TRZEBA było wykorzystać przekrój z przekątną.



 , już wszystko powtórzone tylko z tą stereometrią walcze, ale mam jeszcze troche
czasu żeby ją podszkolić.
, już wszystko powtórzone tylko z tą stereometrią walcze, ale mam jeszcze troche
czasu żeby ją podszkolić.













 , jak zawsze z pytaniami.. Na rysunku Mili widać że promień okregu OPISANEGO
idzie od punktu S
do punktu P to dlaczefo musimy skorzystać z przekroju zawierającego przekątna (pomaranczowy)?
Dlaczefo nie mozna wykorzystać tego zielonego?
Obliczajac PS zamiast PC?
, jak zawsze z pytaniami.. Na rysunku Mili widać że promień okregu OPISANEGO
idzie od punktu S
do punktu P to dlaczefo musimy skorzystać z przekroju zawierającego przekątna (pomaranczowy)?
Dlaczefo nie mozna wykorzystać tego zielonego?
Obliczajac PS zamiast PC?

 Tak btw, tu nie ma okręgów tylko kule w tym zadaniu.
Tak btw, tu nie ma okręgów tylko kule w tym zadaniu.  Bo gdybyśmy chcieli opisać okrąg na tym
trójkącie to zrobiliśmy to tak jak ja na poczatku, wtedy stosunek wyniósłby 2.
Bo gdybyśmy chcieli opisać okrąg na tym
trójkącie to zrobiliśmy to tak jak ja na poczatku, wtedy stosunek wyniósłby 2.

