Plani
Metis:
 Etuś
Etuś
Jak już wyjmiesz tę szarlotkę to zerkniesz na moje zadanka?

1)
http://prntscr.com/avxq7k
2)
http://prntscr.com/avxqdz
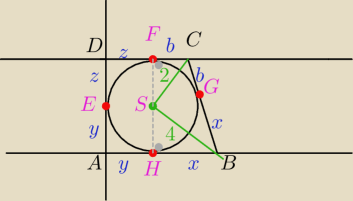
1) W Δ prostokątnym CFS mam:
z
2+b
2=4
−...− SHB mam:
y
2+x
2=16
Wiem też z warunku wpisania okręgu w czworokąt, że suma przeciwległych boków są równe
23 kwi 21:07
Metis: Co do 2) to się bardzo pogubiłem

Obliczyłem wszystkie długości, ale nie mogę wydobyć tych współrzędnych.
23 kwi 21:08
pytajnik123: Metis jaki trójkat CSB jest?

23 kwi 21:08
Metis: Widać, że prostokątny, ale jak to pokazać

?
23 kwi 21:10
pytajnik123: Odcinki BS i CS to dwusieczne prawda? A suma miar kątów przy jednymramieniu wynosi>?

Więc
α+β?

23 kwi 21:13
pytajnik123: Licz teraz ten obwód bo dla Jacka inaczej wyszedł

23 kwi 21:14
prosta:
BS i CS leżą na dwusiecznych kątów wewnętrznych trapezu;
przyjmując przy B : α i α
przy C : β i β
mamy: 2α+2β=180o
α+β=90o
23 kwi 21:15
Metis: No i zadanie ... stało się banalne

Dziękuje

23 kwi 21:16
Eta:
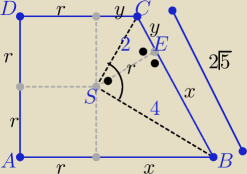
|CB|=
√42+22= 2
√5=x+y
L=4r+2(x+y)=........
23 kwi 21:25
Metis: 
Jeśli możesz to zerknij do 2)
Proszę tylko o wskazówki.
23 kwi 21:27
Eta:

wektory ( nie piszę strzałek
1/ SD= 0,5 AS ⇒ wyznaczysz D(..., ...)
2/ napisz równanie prostej BC ⊥AD i przechodzącej przez punkt D
3/ wyznacz równanie okręgu opisanego na trójkącie ABC ( środkiem jest też punkt S
R= |AS|
4/ rozwiąż układ równań okręgu 3/ z prostą BC i otrzymasz współrzędne punktów B i C
Powodzenia

23 kwi 22:00
23 kwi 22:01
Metis: Teraz już "wejdzie" to zadanie

Dziękujemy
Eta 
(sandomierskie ( podobno najlepsze))

23 kwi 22:02
Mila:
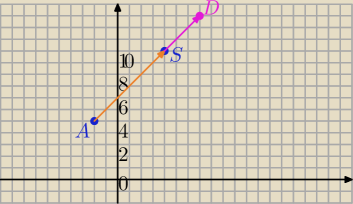
Podpowiedź:
|AS|=2r
AS
→=[6,6]
S=(4,11)→T
[3,3]⇒D=(7,14) środek BC
23 kwi 22:06
Metis: Dobry wieczór
Milu 
Trochę rozłożyliśmy to zadanie i część jest tutaj, a inna część
324360 
23 kwi 22:21
pytajnik123: a
AD=1 ⇒a
BC=−1
BC: y=−x+b
D(7, 14)
14=−7+b
b=21
B(x; −x+21)
Po podniesieniu do kwadratu:
(x−7)
2+(−x+7)
2=54
a z tego x
2−14x+22=0
i Δ=108
?
23 kwi 22:21
Metis: Po prostu:
S to środek okręgu opisanego :
a, |AS|=R
Zatem (x−4)2+(y−11)2=72
23 kwi 22:25
Metis: Wyznacz prostą AD .
Później prostą prostopadłą do AD przechodzącą przez D.
Punkty przecięcia okręgu i tej prostej to nasze współrzędne.
23 kwi 22:28
Metis: Robimy dzisiaj jeszcze jakąś?

23 kwi 22:28
pytajnik123: No wychodzi nam takie samo równanie

23 kwi 22:29
Mila:
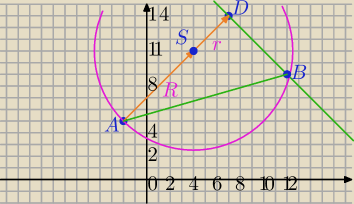
cd. 22:06
SD
→=[3,3] wektor prostopadły do BC:
Równanie ogólne prostej BC:
D=(7,14)
3*(x−7)+3*(y−14)=0
3x−21+3y−42=0
3x+3y−63=0 /:3
BC: x+y−21=0⇔y=−x+21
R=6
√2 − promień okręgu opisanego na ΔABC
S=(4,11)
(x−4)
2+(y−11)
2=(6
√2)
2
(x−4)
2+(−x+21−11)
2=72⇔(x−4)
2+(−x+10)
2=72
x
2−8x+16+x
2−20x+100=72
x
2−14x+22=0
Δ=108
| | 14−6√3 | | 14+6√3 | |
x= |
| lub x= |
| |
| | 2 | | 2 | |
x=7−3
√3 lub x=7+3
√3
y=−7+3
√3+21=14+3
√3
C=(7−3
√3,14+3
√3)
B=(7+3
√3,14−3
√3)
23 kwi 23:01
pytajnik123: Metis masz może gg, albo jakis inny komunikator?
23 kwi 23:02
pytajnik123: Jak widać z długości odcinka wychodzi identycznie

i myślę, że takich wyników trzeba sie na maturze spodziewać

Ładnie raczej wychodzić nie
będzie.
23 kwi 23:03
Jack: 
23 kwi 23:04
Metis: Mila dziękujemy serdecznie


napisałaś się duzo.
23 kwi 23:15
Metis: pytajnik mam GG
23 kwi 23:39
pytajnik123: Napisałem
23 kwi 23:43
Metis: Do kogo

23 kwi 23:43
Eta:
Do mnie

23 kwi 23:43
pytajnik123: Do Metisa chyba xd
23 kwi 23:44
 Etuś
Jak już wyjmiesz tę szarlotkę to zerkniesz na moje zadanka?
Etuś
Jak już wyjmiesz tę szarlotkę to zerkniesz na moje zadanka?  1) http://prntscr.com/avxq7k
2) http://prntscr.com/avxqdz
1) W Δ prostokątnym CFS mam:
z2+b2=4
−...− SHB mam:
y2+x2=16
Wiem też z warunku wpisania okręgu w czworokąt, że suma przeciwległych boków są równe
1) http://prntscr.com/avxq7k
2) http://prntscr.com/avxqdz
1) W Δ prostokątnym CFS mam:
z2+b2=4
−...− SHB mam:
y2+x2=16
Wiem też z warunku wpisania okręgu w czworokąt, że suma przeciwległych boków są równe
 Obliczyłem wszystkie długości, ale nie mogę wydobyć tych współrzędnych.
Obliczyłem wszystkie długości, ale nie mogę wydobyć tych współrzędnych.

 ?
?
 Więc
α+β?
Więc
α+β? 

 Dziękuje
Dziękuje 
 |CB|=√42+22= 2√5=x+y
|CB|=√42+22= 2√5=x+y
 Jeśli możesz to zerknij do 2)
Proszę tylko o wskazówki.
Jeśli możesz to zerknij do 2)
Proszę tylko o wskazówki.
 wektory ( nie piszę strzałek
1/ SD= 0,5 AS ⇒ wyznaczysz D(..., ...)
2/ napisz równanie prostej BC ⊥AD i przechodzącej przez punkt D
3/ wyznacz równanie okręgu opisanego na trójkącie ABC ( środkiem jest też punkt S
R= |AS|
4/ rozwiąż układ równań okręgu 3/ z prostą BC i otrzymasz współrzędne punktów B i C
Powodzenia
wektory ( nie piszę strzałek
1/ SD= 0,5 AS ⇒ wyznaczysz D(..., ...)
2/ napisz równanie prostej BC ⊥AD i przechodzącej przez punkt D
3/ wyznacz równanie okręgu opisanego na trójkącie ABC ( środkiem jest też punkt S
R= |AS|
4/ rozwiąż układ równań okręgu 3/ z prostą BC i otrzymasz współrzędne punktów B i C
Powodzenia 

 Dziękujemy Eta
Dziękujemy Eta  (sandomierskie ( podobno najlepsze))
(sandomierskie ( podobno najlepsze)) 
 Podpowiedź:
|AS|=2r
AS→=[6,6]
S=(4,11)→T[3,3]⇒D=(7,14) środek BC
Podpowiedź:
|AS|=2r
AS→=[6,6]
S=(4,11)→T[3,3]⇒D=(7,14) środek BC


 cd. 22:06
SD→=[3,3] wektor prostopadły do BC:
Równanie ogólne prostej BC:
D=(7,14)
3*(x−7)+3*(y−14)=0
3x−21+3y−42=0
3x+3y−63=0 /:3
BC: x+y−21=0⇔y=−x+21
R=6√2 − promień okręgu opisanego na ΔABC
S=(4,11)
(x−4)2+(y−11)2=(6√2)2
(x−4)2+(−x+21−11)2=72⇔(x−4)2+(−x+10)2=72
x2−8x+16+x2−20x+100=72
x2−14x+22=0
Δ=108
cd. 22:06
SD→=[3,3] wektor prostopadły do BC:
Równanie ogólne prostej BC:
D=(7,14)
3*(x−7)+3*(y−14)=0
3x−21+3y−42=0
3x+3y−63=0 /:3
BC: x+y−21=0⇔y=−x+21
R=6√2 − promień okręgu opisanego na ΔABC
S=(4,11)
(x−4)2+(y−11)2=(6√2)2
(x−4)2+(−x+21−11)2=72⇔(x−4)2+(−x+10)2=72
x2−8x+16+x2−20x+100=72
x2−14x+22=0
Δ=108
 i myślę, że takich wyników trzeba sie na maturze spodziewać
i myślę, że takich wyników trzeba sie na maturze spodziewać  Ładnie raczej wychodzić nie
będzie.
Ładnie raczej wychodzić nie
będzie.


 napisałaś się duzo.
napisałaś się duzo.

