wart
Metis: Funkcja f określona jest wzorem f(x)=|||x|−1|−2|−3 .
Jaka jest największa wartość dla arg. z przedziału <0,4> .
Badam wartości na końcach przedziału − ale czy na końcach tego przedziału funkcja przyjmie
wartość największą?
23 kwi 17:01
ICSP: Wcale nie musi. Weź parabole f(x) = −x2 i przedział [−1 , 1]
23 kwi 17:02
Metis: No właśnie.
Więc jak tu zadziałać ?
23 kwi 17:03
jc: Narysuj wykres i zobaczysz.
23 kwi 17:04
Metis: Znaczy to jest zadanie zamknięte więc mogę sobie podstawiać i sprawdzać.
23 kwi 17:04
ICSP: Skoro jest zamknięte to podstaw wszystkie 4 wartości podane w odp i wybierz największą.
23 kwi 17:06
Metis: Muszę rozwiązać wtedy 4 równania
Myslałem , że mozna szybciej
23 kwi 17:08
ICSP: Narysuj wykres
23 kwi 17:14
pytajnik123: Metis też robisz Arkusz z XI 2015 Wsipu?
23 kwi 17:15
Metis: 
23 kwi 17:17
pytajnik123: Ja dostałem jako pracę domową
Możemy sobie odpowiedzi posprawdzać, bo nigdzie chyba nie ma.
Zamknięte:
1. C
2.B
3. B
4.D
5. A
6. A
7.0, 259
8. 4,17
9. 0,60
10.dowód
23 kwi 17:23
Metis: 1) ok
2) jeszcze nie wstawiałem
3) ok
4. nie liczyłem go jeszcze
5. ok
6. ok
7. 259
8. 4,1666666... proszą o przybliżenie do części setnych zatem 4,17
417
reszta w trakcie.
23 kwi 17:28
Metis: od 5 zaokrąglamy w góre
23 kwi 17:29
Paweł: Te arkusze można znaleźć w internecie?
23 kwi 17:29
pytajnik123: | | π | |
12 chyba namieszałem : x∊{0, |
| , π} |
| | 2 | |
23 kwi 17:33
Metis: w 9) u mnie q=1/3
23 kwi 17:44
pytajnik123: To pewnie źle rozwiązałem układ:
23 kwi 17:48
Metis: Suma wszystkich wyrazów nieskończonego ciągu geometrycznego a
n jest równa 5, a suma
kwadratów wszystkich wyrazów tego ciągu jest równa 6,25. Wyznacz iloraz ciągu a
n.
a
1+a
2+a
3+a
4+... = 5
a
1+a
1q+a
1q
2+a
1q
3...=5
| | a1 | | a1 | |
S= |
| ⇔ |
| =5 ⇔ a1=5(1−q) |
| | 1−q | | 1−q | |
a
12+a
22+a
32+a
42+...=6,25
a
12+(a
1q)
2+(a
1q
2)
2+(a
1q
3)
2+...=6,25
a
12+a
12q
2+a
12q
4+a
12q
4+... =6,25
| | a12 | | a12 | | 25 | |
S2= |
| ⇔ |
| = |
| |
| | 1−q2 | | 1−q2 | | 4 | |
Zatem:
| 25(1−q)2 | | 25 | |
| = |
| |
| (1−q)(1+q) | | 4 | |
25(1+q)=100(1−q)
1+q=4−4q
q+4q=4−1
5q=3 /5
q=0,6
23 kwi 17:52
Metis: Dobrze
23 kwi 17:52
pytajnik123: | | 1 | |
No dokładnie tak samo mam Więc co piszesz, że q= |
| ? |
| | 3 | |
23 kwi 17:53
Metis: Sory
Z szybkości
23 kwi 17:53
Jack: to moze przylacze sie do zabawy...
w zad 13
23 kwi 17:58
Metis: 10) co to za dowód
23 kwi 17:59
pytajnik123: Ja właśnie 10 minut juz myślę nad 13tym i jedyne co mam to układ 4 równań z 4 niewiadomymi
Ale to chyba nie tędy droga
Ale daj jeszcze pomyśleć
23 kwi 18:00
Metis: Nie wstawiajmy rozwiązań. Tylko same wyniki.
23 kwi 18:00
Jack: wystarczy cos zauwazyc
23 kwi 18:02
pytajnik123: | | 28√5+64 | |
Mi wyszedł Obwód: |
| , ale zaraz sprawdzę |
| | 11 | |
23 kwi 18:13
Metis: 14) proste.
Przekształcić do postaci
...>1
23 kwi 18:19
pytajnik123: ja przekształciłem równowaznie do log
23<log
24
Co jest już prawdziwe bo 3<4
23 kwi 18:22
Metis: 16) Trochę rachunków a 7 pkt
23 kwi 18:42
pytajnik123: Ja kiszę w 15tym
Coś chyba na około robię bo to tylko 3 pkt
23 kwi 18:43
Metis: Jeszcze go nie ruszałem
23 kwi 18:44
pytajnik123: To co Ty tak nie po kolei?
23 kwi 18:45
Metis: Nigdy nie rób po kolei !
Robisz te, które umiesz , kojarzysz.
Zaczniesz robisz te, które jest dla Cb problemowe, nie będzie Ci wychodziło, rzucisz go i z
nerwów skopiesz kolejne
Plani zawsze pomijam, potem do niech wracam
23 kwi 18:48
pytajnik123: Sprytne
Bo ja już się wkurzyłem nad nim
I pozostawiłem.
23 kwi 18:49
Metis: No widzisz
23 kwi 18:50
Eta:
|q|<1
| a1 | | a12 | | a1 | | a1 | | 25 | |
| =5 i |
| = |
| * |
| = |
| |
| 1−q | | 1−q2 | | 1−q | | 1+q | | 4 | |
| a1 | | 5 | | 4a1 | | a1 | |
| = |
| ⇒ |
| = |
| ⇒ |
| 1+q | | 4 | | 1+q | | 1−q | |
4−4q=1+q ⇒ 5q=3 ⇒q=0,6
23 kwi 18:55
pytajnik123: Metis w 16tym wspórzędne całkowite wychodzą?
23 kwi 19:00
Metis: Właśnie liczę
23 kwi 19:05
pytajnik123: Okej, daj znać
Bo zatrzymałem się jak mi chcą z pierwiastkiem wychodzić
23 kwi 19:07
Eta:
zad. 14/ ..... czeka .... baaardzo łatwe
23 kwi 19:11
Metis: 14 ) mamy
23 kwi 19:12
Eta:
zad.10 ..... też banalne
23 kwi 19:12
pytajnik123: zad 17
Mi wyszło 147752 liczb
23 kwi 19:12
Metis: zad. 10 ) także mamy
23 kwi 19:13
pytajnik123: Dokładnie
23 kwi 19:13
Eta:
Podaj wynik z zad.14
23 kwi 19:15
pytajnik123: 14 to dowód
23 kwi 19:15
23 kwi 19:15
Eta:
Myślałam,że to zad. info VIII
23 kwi 19:16
Metis: Nie wiem Etuś czy o tych samych arkuszach mówimy.
23 kwi 19:17
Metis:
23 kwi 19:17
Eta:
To podaj wynik zad.14 z info. VIII (
planimetria
23 kwi 19:18
Metis: Jeszcze nie przerabiane
23 kwi 19:18
Eta:
...... "kochana" planimetria
23 kwi 19:20
Jack: Tiaaa kochana ;x
23 kwi 19:21
pytajnik123: Zad 18. h mi wyszło pierwiastek 3 stopnia z 3
23 kwi 19:26
pytajnik123: Eta
| 10√26 | |
| ? |
| 13 | |
23 kwi 19:33
Eta:
ok
23 kwi 19:35
Metis: Ja właśnie liczę 17.
23 kwi 19:36
pytajnik123: Tutaj za 3pkt mamy ciekawsze zadanie
15. W trapezie ABCD, o podstawach AB i CD dwusieczna kąta ostrego o wierzchołku B jest
prostopadła do ramienia AD i dzieli je w stosunku 3:2 licząc od wierzchołka A. Oblicz stosunek
pól figur, na które ta dwusieczna dzieli trapez ABCD.
23 kwi 19:38
pytajnik123: No i jak Metis z tymi współrzędnymi? Całkowite Ci wyszły?
23 kwi 19:39
Jack: Stare...
23 kwi 19:39
Metis: Nie wyszły, za dużo mam danych tam
23 kwi 19:40
pytajnik123: Co stare? Stare zadanie?
23 kwi 19:41
pytajnik123: Jak to za dużo danych? xd
23 kwi 19:41
Jack: Yhyhy
23 kwi 19:44
Metis: Etuś jesteś gdzieś tutaj?
23 kwi 19:56
Metis: pytajnik
17) robiłeś zdarzeniem przeciwnym?
23 kwi 19:57
pytajnik123: Tak, a źle mam? Szybko to robiłem więc mogłem się pomylić
23 kwi 19:58
Metis: Zapisz je tutaj jeśli możesz, muszę rozwiać moje wątpliwosci
Wyszło Ci to z Δ równobocznym ?
23 kwi 20:12
pytajnik123: Nie kończe bo mi współrzędne wychodzą x1=16−6√3 i x2=16+6√3
23 kwi 20:14
pytajnik123: Liczb parzystych bez "5" jest 8*94*5=262440
Wśród nich parzystych bez 4 i 5 jest: 7*84*4=114688
23 kwi 20:16
pytajnik123: A z tym trójkątem plan miałem taki:
1. |AS|=r⇒ można policzyć bok trójkąta
2. z wektorów znaleźć środek boku BC (AS przecież zawiera się w wysokości)
3. Prosta CB jest prostopadła do wysokości stąd współrzędne punktów C i B zapisać można za
pomocą jednej niewiadomej
4 i ułożyć równanie, że długość odcinka np BK (K−środek boku BC) jest równa połowie długości
boku czyli 6
√6
Ale nie wiem czy to jest okej
23 kwi 20:24
pytajnik123: No to arkusz mam zrobiony teraz czekam na korektę błędów
Znalazłem fajny arkusz,
Metis jutro robimy
23 kwi 20:26
Metis: Jaki ?
23 kwi 20:30
pytajnik123: CN Kujawsko −Pomorskie Centrum Edukacji Nauczycieli w Bydgoszczy Marzec 2016
Jak patrzę to
dość ambitny, ale nie zaczynałem jeszcze nic.
23 kwi 20:32
Metis: W tym trójkącie to policzyłem długości wszystkiego
Pola, wysokości, boku, bo można
Ale nie mogę przełożyć tego sensownie dokładne wart. pkt.
Muszę pokombinować z kątem między wektorami.
23 kwi 20:32
Metis: Zrobiłem go już
23 kwi 20:33
Metis: Z tym kombinatorycznym coś źle.
Conajmniej jedna 4 .
Czyli u Nas jedna, dwie, trzy , cztery, pięć lub sześć
Przeciwne − czyli albo bez czwórki , albo jedna 4.
23 kwi 20:35
Metis: Ten bydgoski do łatwych nie należy,
23 kwi 20:35
pytajnik123: Nie no przeciwne to bez 4
23 kwi 20:36
pytajnik123: A− co najmniej jedna czwórka (1, 2, 3, 4, 5 ,6)
A′− zero czwórek
23 kwi 20:38
Eta:
Jestem, jestem
( piekę szarlotkę ..... jak mi się spali , to
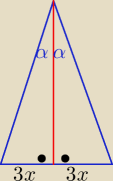
1/ Przedłużam ramiona otrzymując ΔABF podobny do ΔCDF z cechy (kkk)
skoro dwusieczna jest prosto padła do ramienia AD
to |EF|=|AE|= 3k zatem ||DF|=k . k>0
z podobieństwa trójkątów ( wyżej napisałam)
| | 6k | | P(ABF) | | 1 | |
skala s= |
| =6 to |
| =s2=36 ⇒ P(CDF)= |
| P(ABF) |
| | k | | P(CDF | | 36 | |
i P(ABE)=P(EBF)
| P(ABE) | | P(ABE) | | 0,5P(ABF) | |
| = |
| = |
| = |
| P(BEDC) | | P(EBF)−P(CDF) | | | |
| 18P(ABF) | | 18 | |
| = |
| |
| 18P(ABF)−P(ABF) | | 17 | |
23 kwi 20:39
bezendu:
Eta wyślij kawałek do Wrocławia ?
23 kwi 20:40
23 kwi 20:41
pytajnik123: Może ktoś zobaczyć zad 16. Punkt A=(−2, 5) jest wierzchołkiem trójkąta równobocznego ABC, a
punkt S=(4, 11) jest środkiem okręgu wpisanego w ten trójkąt. Oblicz współrzędne wierzchołków
B i C.
Czy współrzędne wyjdą wymierne?
23 kwi 20:45
bezendu: Co kryję się w tych kubkach ?
23 kwi 20:46
Metis: Sok jabłkowy przecież
23 kwi 20:52
Metis: No racja
Tam mamy przynajmniej raz , a nie dwa!
Czyli będzie
23 kwi 20:53
Metis: Pytajnik jak poprowadziłeś trygonometryczne?
Rozpisałeś cos4x?
Bo mało miejsca zostawili, wiec chyba można jakoś szybciej
23 kwi 20:54
pytajnik123: cos4x jako cos(2*2x)
23 kwi 20:55
pytajnik123: cos4x=2cos22x−1
cos22x=(2cos2x−1)2
23 kwi 20:57
Metis: Muszę złapać gdzieś
ZKS tutaj, on jest dobry w te klocki
23 kwi 20:59
pytajnik123: cos4x+2cos2x=1
2cos22x−1+2cos2x=1
cos22x+cos2x=1
(2cos2x−1)2+cos2x=1
4cos4x−4cos2x+1+cos2x=1
cos2x(cos2x−1)=0
23 kwi 21:03
Metis: Ja poszedłem w sin, ale mam analogicznie.
23 kwi 21:09
Metis: Obwód
Jacka jest
23 kwi 21:38
pytajnik123: Wiem, bo jestem idiotą
23 kwi 21:39
Metis: No dobra
23 kwi 21:39
Metis: Chyba jednego jeszcze nie skończyliśmy?
23 kwi 21:43
pytajnik123: No ja jestem ciekaw gdzie mam błąd z tymi współrzędnymi. Spróbuj zrobić tak jak ja pisałem. I
zobacz czy coś z tego wyjdzie Ci.
23 kwi 21:44
Metis: Pierwsze dwa mam dokładnie tak samo.
Z tym, że :
1) najpierw liczę wysokość.
I ze wzoru na wysokość trójkąta równobocznego mam a. Bez użycia promienia.
2) Dokładnie.
Zapisujemy, że |AS|=2|SX| , gdzie X to to środek boku BC.
23 kwi 21:47
5-latek :
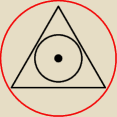
Pytajnik do zadania nr 16 może przyda się wskazowka ze w trojkacie równobocznym srodek okręgu
wpisanego w ten tjkat jest rownie srodkiem okręgu opisanego na tym trojkacie
23 kwi 21:48
pytajnik123: Środek BC wychodzi Ci (16, 23)?
23 kwi 21:49
Metis: Nie, wyszło mi inaczej, chwilka.
23 kwi 21:50
Metis:
No i teraz zapisz.
23 kwi 21:53
pytajnik123: Bo ja dałem: wektor 3AS=AX
23 kwi 21:53
pytajnik123: No tak xd
23 kwi 21:54
pytajnik123: Już poprawiam
23 kwi 21:54
Metis: [AS]=2[SX]
[4+2,11−6]= 2[x−4,y−11]
6=2x−8 , 6=2y−22
2x=14 2y= 28
x=7 y=14
23 kwi 21:56
pytajnik123: tak tak
Gapa jestem
23 kwi 21:57
Metis: I zgadza się . Widać, że ten punkt będzie troszeczkę dalej od S w ukł. wsp.
23 kwi 21:57
5-latek : A
Eta (pozdrawiam
tylko patrzy na to i sie smieje
Zaraz Wam napisze wzory na obrot i po zadaniu
23 kwi 21:59
Metis: To policzmy w woli pewności ten bok:
AX to nasza wysokość.
[AX]=[7+2, 14−5] = [ 9, 9]
|AX|= 9
√2 =h
a
√3=18
√2
23 kwi 22:00
Eta:
Witaj "małolatku"
Właśnie miałam to pisać ...... ( szkoda ,że nie znają równań obrotu
zadanie wtedy rozwiązuje się prawie samo w dwu linijkach
23 kwi 22:02
Metis: Chętnie poznamy!
23 kwi 22:03
23 kwi 22:04
5-latek : 
23 kwi 22:04
23 kwi 22:05
Eta:
tak własnie ten post
23 kwi 22:06
Metis: Etuś powiedz mi jeszcze skąd w zadaniu z dwusieczną mamy:
"skoro dwusieczna jest prosto padła do ramienia AD
to |EF|=|AE|= 3k " − jakoś tego nie widzę,
23 kwi 22:07
Eta:
Znasz własność trójkąta równoramiennego
( wysokość prostopadła do podstawy dzieli podstawę.......
23 kwi 22:09
Eta:
23 kwi 22:12
Metis: Dziękuje
23 kwi 22:20
Eta:
23 kwi 22:20
ZKS:
Metis chodzi o równanie cos(4x) + 2cos2(x) = 1?
23 kwi 23:09
Metis: Cześć
ZKS
tak
Ale pytajnik ma tam błąd:
4cos
4x−4cos
2x+1+cos
2x=1
4cos
4x−3cos
2x=0
cos
2x(4cos
2−3)=0
23 kwi 23:14
Eta:
cos(4x)= 2cos2(2x)−1 = 2(2cos2x−1)2−1
23 kwi 23:18
ZKS:
Hej
Metis.
cos(4x) + 2cos
2(x) = 1
cos(4x) = 1 − 2cos
2(x)
cos(4x) = −cos(2x)
cos(4x) = cos(π − 2x)
4x = π − 2x + k • 2π ∨ 4x = −π + 2x + k • 2π
23 kwi 23:20
Eta:
lub tak
cos(4x)= −(2cos2x−1)
cos(4x)= −cos(2x)
cos(4x)= cos(π+2x)
..................
23 kwi 23:22
Eta:
23 kwi 23:22
Metis: Dzięki
23 kwi 23:35
Metis: cos(4x) = cos(π − 2x) // wzorami redukcyjnymi pozbywacie się minusa?
23 kwi 23:36
Eta:
tak
23 kwi 23:39
Jack: tak jest
− cos x = cos(180 −x )
za to cos(−x) = cos x
23 kwi 23:39
Eta:
Kto Cię tego nauczył
Jacuś
23 kwi 23:40
ZKS:
Ooo
Eta też takie samo rozwiązanie podała.
Tak, przy sinusie jest o tyle łatwiej, że −sin(x) = sin(−x).
Cosinus w drugiej i trzeciej
ćwiartce jest ujemny, dlatego u mnie π − 2x, a
Eta zapisała π + 2x.
23 kwi 23:41
Jack: Jacuś samouk ?
taka pani...z forum
23 kwi 23:41
Eta:
23 kwi 23:42
Metis: π − 2x − druga ćwiartka
π + 2x − trzecia...
Bez różnicy czy to 2x czy x ?
23 kwi 23:46
Eta:
bez
23 kwi 23:50
Jack: Idzcie juz spac dzieciaczki
23 kwi 23:53
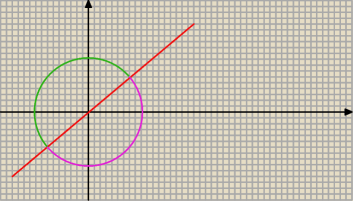
Metis: Jakoś tego nie widzę.
Jeśli do x + π to mamy coś w III
Jeśli do x − π to mamy też III
24 kwi 00:00
Metis:
24 kwi 00:06
Metis: ZKS zapisał cos(π − 2x) = cos(−(π +2x)) korzystam z cos(−x)=cosx
cos(π+2x) , teraz rozumiem
24 kwi 00:22
ZKS:
Może źle się trochę wyraziłem, nie tyle co kąt x jest w II lub III ćwiartce, tylko
wykorzystujemy wzory redukcyjne z II i III ćwiartki, wtedy kąt x może być dowolny, ale będzie
− przed funkcją cosinusem, ponieważ sprowadzamy kąt x do II albo III ćwiartki.
Nie wiem, czy mnie rozumiesz, pisz to postaram się jakoś lepiej Ci to wytłumaczyć.
To po prostu najzwyczajniej w świecie są wzory redukcyjne.
24 kwi 00:26
ZKS:
cos(π − 2x) = cos[−(−π + 2x)] = cos(2x − π)
24 kwi 00:29
Metis: Tak , tylko zrozumiałem, że
Eta umieściła ramię tego kąta w III cwiartce , a ty w II i coś
mi nie trybiło
"Cosinus w drugiej i trzeciej ćwiartce jest ujemny, dlatego u mnie π − 2x, a Eta zapisała π +
2x"
24 kwi 00:29
ZKS:
Tak tutaj się źle wyraziłem. Sprowadziłem kąt z II ćwiartki, tam funkcja jest ujemna jaki
Eta tyle, że sprowadza kąt z III ćwiartki.
Możesz użyć wzorów, aby się przekonać, że kąt x nie ma znaczenia, ale ma znaczenie to z
jakiej ćwiartki sprowadzasz.
cos(π + x) = cos(π)cos(x) − sin(π)sin(x) = −cos(x)
cos(π − x) = cos(π)cos(x) + sin(π)sin(x) = −cos(x)
24 kwi 00:35
Metis: cos(4x) = −cos(2x)
cos(4x) = cos(π − 2x)
cos(4x)= −cos(2x) − a skąd pewność że to II ćwiartka?
czy II/ III
cos(4x)= cos(π+2x)
Ja to widzę tak:
Chcemy pozbyć się tego minusa, więc umieszczamy cos(2x) w III lub II ćwiartce , tam wiemy, że
jest ujemny
Wtedy −(−cos... = cos...
Nie rozumiem zbyt tego sformułowania sprowadzania kąta z ćwiartki.
24 kwi 00:50
Metis: Albo może rozumieć to tak:
−cos(2x) − II/ III ćwiartka a chcemy go własnie z tej II i III ćwiartki sprowadzić.
I teraz wszystko jasne.
Tak trzeba na to patrzeć
24 kwi 00:57
Metis: Rozumiem
ZKS już
Dzięki
Do rana
24 kwi 00:58
ZKS:
Niestety nie jestem nauczycielem, aby poprawnie to Ci sformułować, ale jak sam zauważyłeś
należy umieścić (ja pisałem sprowadzić).
Rozumiesz już coś z tych moich wypocin, czy
dalej nic to postaram się jakoś najbardziej łopatologicznie to napisać.
24 kwi 01:01
ZKS:
Może niezbyt zrozumiale to pisałem, ale chyba zrozumiałeś o co mi chodziło.
Jak będziesz chciał jakieś zadania to napisz gdzieś to Ci coś powrzucam, bo jutro zamierzam
cały dzień spędzić przed komputerem, ponieważ muszę popisać trochę pracy.
Do rana.
24 kwi 01:07
Jack:
24 kwi 09:27
( bo nie mam już