Oblicz pole powierzchni bocznej MMMMM: Podstawą ostrosłupa jest trójkąt równoramienny prostokątny o przeciwprostokątnej długości 2√2. Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 60⁰. Oblicz pole powierzchni bocznej tego ostrosłupa Obliczyłem: ramię trójkąta podstawy (2)

	2
wysokość ostrosłupa		√6
	3

	4
krawędź boczną		√2
	3

I nie wiem czy mam dobre wyniki tych obliczeń

maturzysta: wysokośc ostrosłupa wychodzi √6 Spodek wysokości tego ostrosłupa znajduje się na środku boku przeciwprostokątnej tego trójkąta.

maturzysta: a nie...w sumie...przelicze to jeszcze bo źle narysowałem chyba

maturzysta: Wydaje mi się, że głupoty nie napisałem... bo skoro mamy trojkąt...a jego środke wyznaczają symetralne...to przetną się one idealnie na środku boku przeciwprostokątnej tego trojkąta, co by wskazywało na to, że wysokość tego ostrosłupa jest jednocześnie wysokością ściany bocznej tego boku.... ktoś to musi ocenić jeszcze. Jeśli by tak było to wyokośc ostrosłupa tak jak napisałem, √6

Metis: Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 60^o, zatem dany ostrosłup jest prosty. W ostrosłupie prostym na podstawie można opisać okrąg. W naszym przypadku podstawą jest trójkąt prostokątny ( w szczególności równnoramienny) , zatem spodkiem wysokości naszego ostrosłupa jest punkt leżący na przeciwprostokątnej dzielący ją na 2 jednakowe części ( czytać środek przeciwprostokątnej)

MMMMM: wysokość ostrosłupa "wychodzi" z punktu przeciecięcia się środkowych trójkąta? Dziękuję

Metis: 323517

maturzysta: Czyli tak jak pisałem. W poleceniu mamy krawędź boczna, a gdyby napisali ściana boczna to wychodze z założenia, że nie da się takiego ostrosłupa zbudować gdzie ściana boczna nachylona pod kątem 60

maturzysta: MMMMMM nie środkowych, tylko symetralnych. Symetralne wyznaczają środek.

MMMMM: Dziękuję

maturzysta: Jeśli chcemy opisać na trójkącie okrąg to wyznaczamy jego symetralne. A gdy chcemy wpisac okrąg w dany trojkąt to wyznaczamy wtedy jego dwusieczne.

MMMMM: Jeszcze raz dziękuję.

Metis: Twierdzenie o ostrosłupie prostym jest jednoznaczne: Przytoczę je: Def: Ostrosłupem prostym nazywamy ostrosłup spełniający dwa warunki: 1) Na podstawie tego ostrosłupa można opisać okrąg 2) Spodek wysokości ostrosłupa jest środkiem okręgu opisanego na podstawie. Oraz: 1^o Ostrosłup jest ostrosłupem prostym ⇔ 2^o wszystkie krawędzie ostrosłupa są jednakowej długości ⇔ 3^o wszystkie krawędzie boczne tworzą jednakowe kąty z płaszczyzną podstawy. W zadaniach rzadko umieszczają informację, że jest to graniastosłup prosty. Zawierają informację 2^o lub 3^o , a ty wnioskujesz najpierw 1^o , a później powołujesz się na def. ostrosłupa prostego.

MMMMM: Mam dalej problem jak obliczyc wysokośc ściany bocznej o podstawie przyprostokątnej

MMMMM: to tu wszystkie krawędzie boczne są równe

Metis: Zrób sobie porządny rysunek. Trójkąt prostokątny równoramienny , opisz na Nim okrąg. Zaznacz wysokość i wykreśl ostrosłup. Zaznacz kąty. Wszystko pięknie widać.

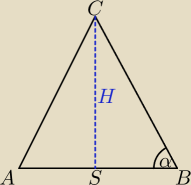
Metis: S=spodek wysokości ostrosłupa H |AS|=|SB| , |AB|− przeciwprostokątna α=60^o

MMMMM: Rysunek mam. Dziękuję

Metis: Jeśli trzeba będzie pomóc to będę tu o 5:00 , zajrzę. Tymczasem Dobranoc

MMMMM: jak obliczę pole boczne, to wstawię wynik Dzięki za poświęcony czas

MMMMM: a ramię h bocznej ściany wynosi

	a
h2=(		)2+H2
	2

h=√7

	a*h		(2√2)2*√3
P=2*		+		=2√7+2√3=2{√7+√3)
	2		4

maturzysta: http://s31.postimg.org/sgkrtlaq3/WP_20160423_01_27_41_Pro.jpg Zgadza sie.

MMMMM: Bardzo dziękuję. Dziś dużo się nauczyłem

maturzysta: Nie ma sprawy. Ten przypadek ostrosłupa gdy podstawą jest trójkąt prostokątny do zapamiętania.

Metis: Przytoczę jeszcze jedno twierdzenie dotyczące ostrosłupów, które uważam za ważne Jeśli wszystkie ściany boczne ostrosłupa są jednakowo nachylone do płaszczyzny podstawy,to spodkiem wysokości ostrosłupa jest środek okręgu wpisanego w podstawę

Evelek: A jeśli podstawą ostrosłupa jest trójkąt prostokątny to wysokość ostrosłupa jest jednocześnie wysokością ściany bocznej najdluzszego boku i znajduje sie ona idealnie w jego połowie. Dowód: Trójkąt prostokątny wpisany w okrąg: jego najdłuższy bok zawsze będzie średnicą tego okręgu a symetralne tego trójkąta przetną się idealnie w środkowym punkcie tego okręgu czyli w połowie długości przeciwprostokątnej tego trójkąta. Warte zapamiętania myślę aby potem nie myśleć za długo na maturze czy na pewno tak może być.