stożek, pole boczne Malwina: trójkąt prostokątny o przyprostokątnych 5cm i 12 cm obraca się wokół dłuższej przyprostokątnej. Jakie jest pole boczne powstałej bryły?

Malwina: Wg mnie: l = 5 r = 12 Pb = πrl = π * 12 * 5 = 60π

Jerzy: 65π

Malwina: jak to?

Malwina: jak to obliczyć?

Jerzy: r = 5 l = 13

Malwina: aaa, jaki głupi błąd zrobiłam dzięki

Malwina: Mam jeszcze 2 takie krótkie zadanka: 1. Trójkąt o wysokości 2 pierwiastki z 3 stanowi przekrój osiowy stożka. Pole boczne tego stożka jest równe...? 2.Przekrój osiowy walca jest kwadratem o przekątnej 6 pierwiastków z 2. Pole boczne walca wynosi...? 1. ze wzoru na wysokość a = 4 Pb = πrl = 8π 2. skoro przekątna to 6 pierwiastków z 2, to a = 6, a r = 1/2a = 3 Pb = 2πrH = 36π Możecie sprawdzić, czy dobrze?

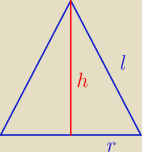
Janek191: h = 2√3 Mało danych r = ?

Janek191: Może to jest trójkąt równoboczny ?

dero2005: 1. Czy tojest trójkąt równoboczny?

Malwina: tak, równoboczny, przepraszam! zjadłam słowo:(

Janek191: z.2 ok

Malwina: a to pierwsze też jest ok?

Janek191: Jok

Malwina: Super, dzięki za sprawdzenie! Janek, miałabym jeszcze prośbę. Dodałam wczoraj zadanie: https://matematykaszkolna.pl/forum/323681.html Czy wynik jest poprawnie zapisany? Mógłbyś zajrzeć raz jeszcze, jeśli znalazłbyś chwilkę?

Malwina: r = (5√2π)/2π to r² nie powinno wyglądać tak: 50π/4π² ?