#WORKOUT PrzyszlyMakler: 1)Z pojemnika zawierającego 10 kul białych i 6 czarnych losujemy jedną kulę i wkładamy zamiast niej jedną kulę czarną. Oblicz prawdopodobieństwo tego, że jeżeli teraz wylosujemy z pojemnika dwie kule, to obie wylosowane kule będą białe.

	10		10		100
Ja bym to zrobił..		*		=
	16		16		256

Ale wyczuwam jakiś haczyk.. 2) oblicz

	x2 −2x
limx→2
	√x+2 −2

Wyszło mi +niesk, ale nie jestem pewien. Mógłby ktoś policzyć, a jeżeli uzyskacie inny wynik to przedstawie swoje obliczenia i ustalimy gdzie jest błąd? Bardzo proszę.

PrzyszlyMakler:

	10		9
1) oczywiscie		*		= 90/256
	16		16

Mila: 2) Przekształcam:

x*(x−2)		√x+2+2		x*(x−2)*(√x+2+2)
	*		=		=
√x+2−2		√x+2+2		x+2−4

	x*(x−2)*(√x+2+2)
=		=x*(√x+2+2)
	x−2

lim_x→2[x*(√x+2+2)]=2*(√2+2+2)=8

PrzyszlyMakler: Doszedłem do postaci x(√x+2 +2) i jakimś cudem uznałem, że x→∞, więc mam ∞ + ∞.. Echh...

PrzyszlyMakler: A Milu, czy pierwsze dobrze? Oczyywiście bardzo dziękuję za granicę.

Mila: Nie wydaje mi się, aby było dobrze. Policzyć?

Mila: Liczyłam to chyba Metisowi, ale wyszukiwarka źle działa i nie mogę znaleźć.

PrzyszlyMakler: Przedstaw co należy zrobić, bo nie rozumiem o co chodzi w tym zadaniu do końca.. Trzeba wylosować dwie białe kule. Losując jedną z 10 białych na 16 łącznie to robię to na 10/16, a potem wkładam jedną czarną, więc kul wciąż jest 16, a białych jedna mniej, więc 9/16..

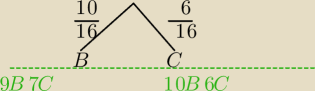
Mila: Dobrze zaczynasz. Teraz tak:

	10		9 2		6		10 2
P(BB)=		*		+		*		=
	16		16 2		16		16 2

	5		4*9		3		5*9
=		*		+		*		=
	8		8*15		8		8*15

	21
=
	64

sprawdź rachunki albo odpowiedź.

PrzyszlyMakler: Rozumiem. Po prostu nie zrozumiałem treści. Myślałem, że uznajemy możliwości tylko otrzymania dwóch białych. A to trzeba było zrobić, że najpierw obojętnie jaka, a potem dwie białe. Trochę niejasne. Dziękuję!

Mila: Zawsze w takim przypadku rysuj "kawałek" drzewka, to jest doświadczenie losowe dwuetapowe, od wyniku z I etapu zależy wynik z drugiego etapu.

Metis: 322411

Mila: Jest niezawodny Metis.

Metis:

Mila: Jak tam geometria? Z algebrą ładnie sobie radzisz.

Metis: Dobry wieczór Milu Algebrę lubię Z planimetrią już tak wesoło nie jest − przypominam sobie podstawowe własności, związki , i przejrzę rozwiązane zadania na zadania.info i z poprzednich matur. I to będzie na tyle. W tej kwestii już raczej nic nie zdziałam, mam za duże braki. Może jeszcze uda mi się zabrać Etę na maturę Na swojej liście mam jeszcze parę tematów do odświeżenia, walczę Żałuję, że nie udało mi się wygrać tego indeksu Zadanie z III etapu nie były takie skomplikowane, ale mówi trudno, teraz miałbym święty spokój. Gdy wrócę jutro ze szkoły wróce do twoich zadań. Miałem pojechać na dni otwarte AGH, ale szkoda mi całego dnia. Zad.3 − z układem mam skończone Powalczę z zad . 2 i spróbuje od nowa popatrzeć na okrąg z kątami wpisanymi.

Mila: Musisz dać linka do tych zadań, bo nie wiem, gdzie są. Mogę Ci napisać kilka nowych, niezbyt wymyślnych, ale pożytecznych. Wpisuj zadania z trudnościami. Zobacz na dowody , które napisałam Ralfowi, są dość podstawowe. W geometrii trzeba rysować i "patrzeć." Staraj się też pisać komentarze z dobrą interpunkcją, jako ćwiczenie przed maturą. Mnie to nie przeszkadza, ale ucz się kompleksowo. No to cała naprzód!

Metis:

Mila: Dobranoc

PrzyszlyMakler: Zazdroszczę wiedzy Metis, jeżeli tamte zadania z AGH są naprawdę dla Ciebie łatwe ; ). W takim razie nie masz się czego obawiać na maturze ; )