#workout PrzyszlyMakler: 1)Z urny w któej jest 8 białych i 6 czarnych kul losujemy bez zwracania dwie kule. Oblicz prawd. że za drugim razem wylosowana została czarna kula, jeżeli za pierwszym wylosowana była biała.

	8		6		48
Zrobiłem		*		=		Git?
	14		13		182

2) Prosta o równaniu x − 2y + 2 = 0 przecina okrąg o równaniu x² + y² − 6x − 10 = 0 w punktach A i B. a)Oblicz dlugosc cieciwy tego okregu zawartej w danej prostej. b)Napisz równanie symetralnej cięciwy AB. x = 2y − 2 Po podstawieniu: 5y² −20y + 6 = 0

	10 + √70
y1 =
	5

	10 − √70
y2 =
	5

I trochę spanikowałem. Podstawiając do x − 2y + 2= 0 najpeirw y1 potem y2 będe miał dwie cięciwy. Która jest zawarta w danej prostej?

Jack: w zad. 1 wylosowales juz biala, a Ty liczysz jak bys mial ja dopiero wylosowac. jako ze sam mam duzo problemow, to nie wiem czy git, ale ja bym zrobil tak : skoro juz biala wylosowallismy, to zostalo 7 bialych i 6 czarnych

	6
wiec prawdopodobienstwo =
	13

https://matematykaszkolna.pl/forum/317164.html

PrzyszlyMakler: Czaję.. To ma sens. Ale i tak chore. Takich zadań nie powinno być. xD

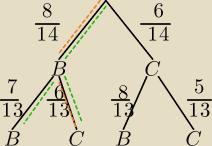
Mila: 1) A− za drugim razem wylosowano czarna kulę B−za pierwszym razem wylosowano białą A∩B− za pierwszym razem wylosowano białą i za drugim razem wylosowano czarna kulę

	8		7		8		6		8*7+8*6
P(B)=		*		+		*		=		⇔
	14		13		14		13		14*13

	104		8		4
P(B)=		=		=
	14*13		14		7

	8		6		48		24
P(A∩B)=		*		=		=
	14		13		14*13		7*13

	24   7*13		24		7		6
P(A/B)=		=		*		=
	4   7		7*13		4		13

prosta: 2) po podstawieniu będziesz miał dwa punkty, które są końcami cięciwy Łatwiej jest policzyć odległość środka okręgu od danej prostej i potem policzyć długość połowy cięciwy z Pitagorasa

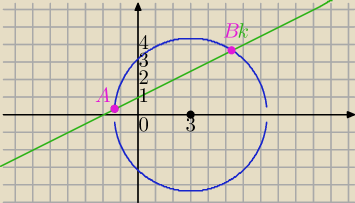
Mila: 1) Prosta o równaniu x − 2y + 2 = 0 przecina okrąg o równaniu x² + y² − 6x − 10 = 0 w punktach A i B. x² + y² − 6x − 10 = 0⇔ (x−3)²−9+y²−10=0 (x−3)²+y²=19 , r=√19

	1
k: x−2y+2=0⇔ k: y=		x+1
	2

2) x² + y² − 6x − 10 = 0 i x−2y+2=0, x=2y−2 (2y−2)²+y²−6*(2y−2)−10=0 4y²−8y+4+y²−12y+12−10=0 5y²−20y+6=0 Δ=280 √Δ=2√70

	20−2√70		10−√70		10−√70		10−2√70
y=		=		to x=2*		−2=		<0
	10		5		5		5

	10−2√70		10−√70
A=(		,		)
	5		5

lub

	10+√70		10+√70		10+2√70
y=		to x=2*		−2 , ⇔x=
	5		5		5

	10+2√70		10+√70
B=(		,		)
	5		5

	10+2√70		10+√70		10−√70
|AB|2=		−(10−2√70}{5}))2+(		−(		))2
	5		5		5

	4√70		2√70
|AB|2=(		)2+(		)2
	5		5

	16*70+4*70		70*20
|AB|2=		=		=14*4
	25		25

|AB|=2√14 ====== Rzeczywiście wredne zadanie. Ciekawa jestem, czy zgodne z odpowiedzią.

Mila:

PrzyszlyMakler: Milu, a po co zwijałaś ten wzór? Przecież położenie okręgu nam nic nie daje. A w drugim podpunkcie nie wiem skąd wiedziałaś, które punkty podstawić. I w 2 trzeba było napisać równanie symetralnej cięciwy.

Mila: 1) Zwijałam, aby narysować, na kartce też możesz naszkicować. 2) Ponadto potrzebny środek okręgu do równania symetralnej. Rysunek zawsze pomaga. Możesz np. stwierdzić w przybliżeniu jakie są wsp. punktów przecięcia. Na ogół w zadaniach wychodzą ładniejsze wyniki. 3) Środek cięciwy jest ładny, symetralna cięciwy przechodzi przez środek okręgu ([N[Qulka pisała]]) i środek cięciwy − S_cięciwy =(2,2) 4) Piszesz równanie prostej przechodzącej przez punkty: (2,2) i (3,0)

PrzyszlyMakler: Ok. Dziękuję.