22 dni
Metis:
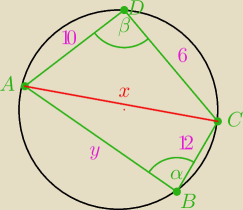
Na czworokącie ABCD można opisać okrąg. Długości boków tego czworokąta są równe:
|BC|=12 , |CD|=6, |AD|=10, a kąt ABC ma miarę 60
o. Oblicz długość promienia okręgu opisanego.
α=60
o
Szukam brakującej długości boku |AB|=y.
Na podst. tw. o czworokącie wpisanym w okrąg:
β=180
o−60
o=120
o
Na pods. tw. cosinusów w ΔACD:
x
2=10
2+6
2−2*10*6*sin(30
o)
oraz
w ΔABC:
x
2=y
2+12
2−2*12*y*cos(60
o)
otrzymuję:
10
2+6
2−2*10*6*sin(30
o) = y
2+12
2−2*12*y*cos(60
o)
100+36−60=y
2+144−12y
y
2−12y+144−76=0
y
2−12y+68=0
brak miejsc zerowych
Gdzie robię błąd?
11 kwi 17:46
===:
sprawdź znaki w tym pierwszym równaniu cosinusów
11 kwi 17:52
Metis: | | 1 | |
cos(120o)=(90o+30o)=sin(30o) = |
| = cos(60o) |
| | 2 | |
Jeśli o to chodzi.
11 kwi 17:55
Jack: Blad...
W drugiej tylko sinus jest dodatni...zatem?
11 kwi 17:57
Jack: cos 120 = cos (90+30) = − sin 30
11 kwi 17:58
Mila:
| | 1 | |
cos(120o)=cos(180o−60o)=−cos60o=− |
| |
| | 2 | |
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Skorzystaj z tw. sinusów w ΔADC:
x=..
Potem tw. cosinusów.
Napisz, czy wyszło dobrze.
11 kwi 17:59
Metis: 
Dzięki.
11 kwi 17:59
Metis: Witaj Milu
Nie mam do tego odp. ale już sobie poradzę
11 kwi 18:01
===:
... no już przestań stukać
11 kwi 18:04
Metis: 
11 kwi 18:05
Jack: odliczasz?
11 kwi 18:07
Metis: A daj spokój
11 kwi 18:07
Metis: Milu , a czy nie lepiej obliczyć od razu x z tw. cosinusów w ΔACD i uzyć tw. sinusów do
obliczenia promienia?
11 kwi 18:10
Mila:
Trzy zadania z planimetrii.
1)
Oblicz pole trójkąta, w którym dwie środkowe o długościach a i b przecinają się pod kątem α.
2)
Na przedłużeniu przeciwprostokątnej AB trójkąta prostokątnego obrano punt D tak, że |BD|=|BC|.
Oblicz |CD|, jeżeli wiadomo, że |BC|=a,|AC|=b.
3)
Oblicz długości boków trójkąta prostokątnego, którego obwód wynosi 70 a pole 210.
11 kwi 18:11
Mila:
Metis, wypróbuj obydwa sposoby. Potem decydujesz co szybciej.
11 kwi 18:13
Jack: jak ja mam dosc matmy na dzis.
11 kwi 18:14
Metis: Dokończę
Na podst. tw. cosinusów w ΔACD:
x
2=10
2+6
2+2*10*6*sin(30
o)
x
2=100+36+60
x
2=196 ⇔ x=14
Na podst. tw. sinusóww ΔABC:
==============================================
11 kwi 18:18
11 kwi 18:20
kyrtap: Panowie to tylko matura
11 kwi 18:30
Metis:
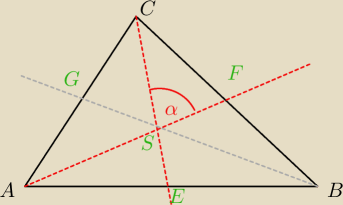
1) Oblicz pole trójkąta, w którym dwie środkowe o długościach a i b przecinają się pod kątem α.
Niech |CE|=a oraz |AF|=b, wtedy:
oraz
| | 1 | | 1 | | 2a | | b | |
Zatem PΔSFC= |
| * |SC| * |SF| * sinα = |
| * |
| * |
| *sinα |
| | 2 | | 2 | | 3 | | 3 | |
Korzystając z wł. środkowej :
P
ABC= 6 * P
ΔSFC
11 kwi 18:51
Metis: 3) Oblicz długości boków trójkąta prostokątnego, którego obwód wynosi 70 a pole 210.
Niech a,b,c będą długościami ramion trójkąta prostokątnego ABC, gdzie c to przeciwprostokątna
P
ΔABC=210
a*b=420
L=70
a+b+c=70
Z tw. Pitagorasa:
c=
√a2+b2
Układ równań:
a*b=420
a+b+
√a2+b2 =70 −−−−−−−− ale na pewno można prościej
11 kwi 18:55
Metis: Siemka
kyrtap
długo Cie nie było
11 kwi 18:57
Mila:
1) Bardzo ładnie
3) zbyt skomplikowane będziesz miał obliczenia
Jest kilka sposobów:
1) np.
a+b=70−c /
2 z tego obliczysz c
a*b=420
2) obliczyć promień okręgu wpisanego z wzoru P=p*r
i rysunek pomoże.
11 kwi 19:11
Metis: Właśnie kombinowałem z promieniem
Wiemy, że P=rp , gdzie p to połowa obwodu , stąd r= 6
11 kwi 19:13
Mila:
Policz pierwszym sposobem, a potem będziemy korzystać z promienia.
Różne sposoby mogą się przydać, powtarzasz w ten sposób zastosowanie własności figur.
11 kwi 19:21
Metis: A to wskazówka do 2
Myślałem o 3
11 kwi 19:22
Mila:
To 19:13 podałam do (3). Podaj wynik.
Z drugim masz problem?
11 kwi 20:12
Metis: Przepraszam Milu, awaria prądu na całym osiedlu.
Nad II jeszcze nie myślałem− nie robiłem rysunku.
Zająłem się tym zadaniem z ciągami.
11 kwi 20:41
kyrtap: nie było bo zapracowany
11 kwi 21:46