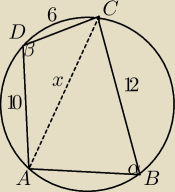
okrag opisany na czworokacie sagan: Na czworokącie ABCD można opisać okrąg. Długości boków tego czworokąta są równe |BC|=12, |CD| = 6, |AD| =10, a kąt ABC ma miarę 60 stopni . Oblicz długość promienia okręgu opisanego na czworokącie ABCD.

irena_1: α=60⁰ β=180⁰−α=120⁰ Z twierdzenia cosinusów dla trójkąta ACD:

	1
x2=102+62−2*10*6*cos1200=136−120*(−		)=136+60=196
	2

x=14 R− promień okręgu opisanego na czworokącie ABCD (oraz na trójkącie ACD) Z pola trójkąta ACD:

	1		√3
P=		*10*6*sin1200=30*		=15√3
	2		2

	10*6*14		210
P=		=
	4R		R

210
	=15√3
R

	210		14		14√3
R=		=		=
	15√3		√3		3

Eta: x=14

	14		14√3
z tw. sinusów w ΔABC		=2R ⇒ R=
	sin60o		3

kasia: Eta pomozesz mi rozwiazac te rownania? 4x−2y=6 3x+6y=12 2x−3y=−5 −x+5y=6 x=y=3 x−2=6

Mila: 4x−2y=6 /*3 3x+6y=12 −−−−−−−−−−−−−−− 12x−6y=18 3x+6y=12 −−−−−−−−−−−− dodajemy stronami 15x=30 /:2 x=2 podstawiamy do II równania 3*2+6y=12 6y=12−6 y=1 x=2 i y=1 Spr. L₁=4*2−2*1=8−2=6=P₁ L₂=3*2+6*1=6+6=12=P₂