Wyznacz równanie prostej Klaudia: Okrąg o środku S (12, 7/2) ) lezy wewnątrz okręgu o równaniu (x−6)²+(x−8)²= 100 i jest do niego styczny. Wyznacz równanie prostej stycznej do obu tych okręgów.

Metis: 1) Popraw równanie okręgu. (Przyjmuję, że (x−6)²+(y−8)²= 100 2) Znajdź równanie prostej k przechodzącej przez punkt S i S', gdzie S(12, 3.5) i S'( 6,8) . 3) Znajdź pkt. A przecięcia okręgu z danym promieniem i prostą k . 4) Szukaną styczną jest prosta prostopadła do prostej k przechodząca przez A.

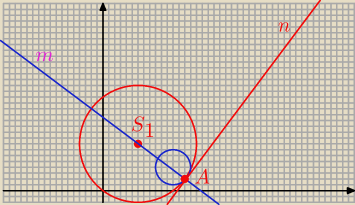
Janek191: S =( 12; 3,5 ) S₁ = ( 6, 8) Prosta SS₁

	4,5		9
a =		= −		= − 0,75
	−6		12

y = − 0,75 x +b 8 = −0,75*6 + b b = 8 + 4,5 = 12,5 m : y = −0,75 x + 12,5

	4
n : y =		x + b1
	3

Klaudia: Z którego wzoru obliczyć punkt przecięcia?

Metis: Oczywiście chodzi o punkt styczności, − punkty wspólny. 321617