Prosta pochodna Marian :

k2 + 4
	Wyznacz ekstrema. Nie wiem dlaczego mi wychodzi wartość maksymalna dla k= −2 a
k

minimalna dla k = 2 a nie odwrotnie sprawdzam po kilka razy i nie wiem gdzie mam błąd

Marian : Napewno mam jakiś banalny błąd ale nie mogę go znaleźć

Marian : https://matematykaszkolna.pl/forum/290425.html o to zadanie mi chodzi. Czyli jednak dobrze liczę ekstrema ale nadal nie rozumiem jak mam wyznaczyć te sumę

Marian : Pomoże ktoś Wychodzi na to że k przyjmuje największą wartość gdy zbliża się z prawej strony do zera

Godzio:

	k2 − 4
f'(k) =		> 0 ⇒ (k − 2)(k + 2)k > 0
	k

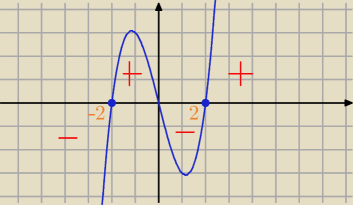
Dla k = −2 jest minimum lokalne, dla k = 2 jest maksimum lokalne

Godzio:

	k2 − 4
No i myła ...		> 0 ⇒ (k − 2)(k + 2) > 0
	k2

Więc w k = 2 jest minim, a w k = 2 maksimum

Godzio: k = −2 maksimum*

Godzio: kx² − (k²+4)x + 1=0 Δ = (k² + 4)² − 4k² = k⁴ + 8k² + 16 − 4k² = k⁴ + 4k² + 16 > 0 k ≠ 0

	k2 + 4		4
x1 + x2 =		= k +
	k		k

Biorąc dowolnie duże k suma pierwiastków jest dowolnie duża i nie trzeba liczyć do tego pochodnej.

Marian : Więc zadanie nie ma rozwiązania W odpowiedziach: Suma jest najmniejsza dla k=−2 a największa dla k= 2

Marian :

Marian: pomoże ktoś?

Marian: ?

Marian : ?

Godzio: Nie ma rozwiązania, najmniejsza jak i największa nie istnieją.

Marian : Dzięki! czyli w książce jest błąd