pochodna Kasia: równanie kwadratowe kx²−(k²+4)x+1=0 ma dwa różne pierwiastki. znajdż tę wartość parametru k, dla której suma pierwiastków danego równania jest najmniejsza oraz tę wartość parametru k, dla której suma pierwiastków jest największa. Dla znalezionych wartości parametru oblicz sumę pierwiastków

	k2+4		k2−4
rozwiązywałam to tak : g(x)=		g`(x)=		znjaduję miejsca zerowe pochodnej
	k		k2

k=2, k=−2 i wychodzi mi że pochodna zmienia znak z + na − w x=−2 czyli ze tam jest maksimum, a przecież jest odwrotnie, w x=2 jest maksimum

Janek191: Δ = ( k² + 4)² − 4 k*1 = k⁴ + 8 k² +16 − 4 k = k⁴ + 4 k² + 16 > 0 dla k ∊ ℕ

	− b		k2 + 4
x1 + x2 =		=
	a		k

	k2 + 4		4
g(k) =		= k +
	k		k

	4
g '(k) = 1 −		= 0 ⇔ k = − 2 lub k = 2
	k2

	8
g''( k ) =
	k3

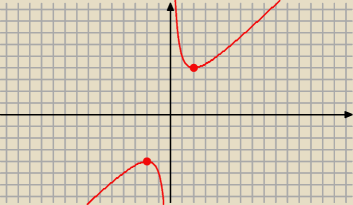
więc g ''( − 2) = − 1 < 0 − więc funkcja g osiąga maksimum lokalne dla k = − 2 g''( 2) = 1 > 0 − więc funkcja g osiąga minimum lokalne dla k = 2

Kasia: ale to jest tylko minimum lokalne, więc nie mogę jeszcze powiedzieć ze suma pierwiastków jest tu najmniejsza w całej dziedzinie, czyli wynikałoby z tego że zadanie nie ma rozwiązania?

Marian : Mam taki sam problem jak Kasia wyjaśni ktoś?

Marian : Też mi się wydaje że to zadanie nie ma rozwiązania

Janek191: Masz Suma pierwiastków z wzorów Viete'a jest równa

	− b		k2 +4		4
x1 + x2 =		=		= k +
	a		k		k

	4
Niech g(k) = k +
	k

Szukam maksimum lokalnego i minimum lokalnego tej funkcji

	4
g '(k) =1 −		= 0 ⇔ k = − 2 lub k = 2
	k2

Obliczam drugą pochodną

	8
g ''(k) =
	k3

	8
Ponieważ g '' (−2) =		= − 1 , więc funkcja g osiąga dla k = − 2 maksimum
	− 8

	4
lokalne równe g(−2) = −2 +		= − 4
	−2

	8
Ponieważ g ''( 2) =		= 1 > 0 , więc funkcja g osiąga dla k = 2 minimum lokalne
	8

	4
równe g(−2) = 2 =		= 4
	2

Reszta na wykresie wyżej