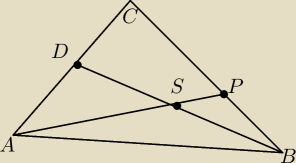
Trójkąt, udowadnianie twierdzenia. Pw: W trójkącie ABC, gdzie |CB| = a, poprowdzano środkową |BD| z punktu B na bok |AC|. Przez punkt S który jest środkiem odcinka |BD| i punkt A poprowdzano prostą, która przecięła bok |BC| w punkcie P. Udowodnij że |PC| = 2/3a.

mat16: 319211

g: Potraktujmy punkty jako pary współrzędnych, np. A=(A_x,A_y).

	A+C   B+   2
W sposób skrócony można napisać: S =
	2

Punkt P leży na przedłużeniu odcinka AS, co można zapisać: P = A + (S−A)*t gdzie t jest jakąś, na razie nieznaną liczbą. Punkt P leży też na odcinku BC, co można zapisać: (P−B) x (P−C) = 0 ('x' − mnożenie wektorowe) Po dość prostych rachunkach można wyznaczyć, że t = 4/3. Stąd wiadomo gdzie jest P.

	2(B−A) + (C−A)
P = A +
	3

I dalej: P−C = 2/3 (B−C) P−B = −1/3 (B−C)

mat16: "pokrętny" ten dowód