#workout 13 PrzyszlyMakler: Wykaż, że dla każdego kąta α prawdziwa jest róność 2(sin⁴α + cos⁴α) = 2 − sin²2α Dla mojego łatwiejszego pisania przyjmę α=x L= 2(sin⁴x + cos⁴x) = =2[(sin²x + cos²x)² − 2sin²x*cos²x]= =2[(sin²x + cos²x)² − (√2sin²x*cos²x)²] = =2[(sin²x + cos²x − √2sin²xcos²x)(sin²x + cos²x + √2sin²xcos²x)] z jedynki tryg. =2[1² − (√2sin²xcos²x)²] = L= 2 − 4sin²xcos²x P= 2 − sin²x = 2 − 2sin²xcos²x L≠P Gdzie błąd?

Benny: 2(sin⁴x+cos⁴x)=2[(sin²x+cos²x)²−2sin²xcos²x]=2(1−2sin²xcos²x)=

	1
=2(1−		sin22x)=2−sin22x
	2

Eta: L= 2(sin²x+cos²x)²−4sin²x*cos²x = 2−sin²(2x)=P

PrzyszlyMakler: Ok Dziękuję. Dany jest trójkąt ABC, w którym odcinek BD jest środkową, punkt E jej środkiem. Przez punkt E i wierzchołek A poprowadzono prostą, która przecięła bok BC w punkcie F. Wykaż,

	2
że CF =		BC
	3

PrzyszlyMakler: #pOMOCy

Eta: Chwila moment już rysuję

PrzyszlyMakler: Dziękuję. Ja sobie narysowałem nawet w rzeczywistych wymiarach ten rysunek i rzeczywiście tak jest! Szukałem trójkątów podobnych, przystających, ale jedyne do czego doszedłem, to to, że środkowa dzieli trójkąty o równych polach, ale nie wiem co z tym zrobić.. Kątów się żadnych nei doszukałem, ani trójkątów podobnych.. Tragedia te dowody, nie wiem czy sie ich nawet uczyc przed matura, bo chyba bym musial 2 miesiece sie uczyc, by zrobic jakies zadanie z rozszerzenia z dowodu− szczegolnie geometrycznego..

PrzyszlyMakler: Najgorsze jest to, że jestem pewien, że trzeba znaleźć jakieś trojkaty podobne, A Ty, Droga Eto narysujesz zaraz ten rysunek, pokażesz mi trójkąty podobne i palne sobie w łeb..

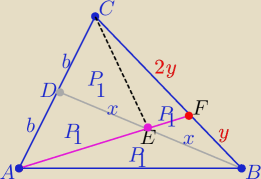
Eta: Dasz radę napisać komentarze do tego rysunku? z własności środkowych ED w ΔAEC i BE w ΔABC i CE w ΔBDC ..................................... ..................................

	1
zatem P(BEC)=		P(ABC) i z tego wynika teza, że |FC|=2y i |FB|=y
	4

	2
to |FC|=		|BC|
	3

co kończy dowód

PrzyszlyMakler: Skąd wiemy, że środkowa CE jest środkową trójkąta BDC?

Eta: Z treści zadania "punkt E jest jej środkiem .. tzn. środkiem BD"

PrzyszlyMakler: Ale skąd wiemy, że odcinek E jest środkiem DB? Tego nie ma w treści.

Eta: No przecież masz tę informację w treści zadania! ( czytanie ze zrozumieniem?

Eta: Jasne? czy jeszcze nie?

PrzyszlyMakler: Tak.. oczwiście. XD jeju. Ale hmm. I tak nie za bardzo rozumiem co z tego wynika. W sensie.. dlaczego to udowodniłaś.

Eta: 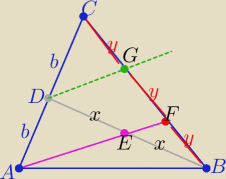Inny sposób Prowadzimy prostą DG ∥ AF Z twierdzenia Talesa w ΔAFC : |FG|=|GC|=y analogicznie w trójkącie BDG : |GF|=|FB|=y

	2
to: |CF|=2y i |FB|=y ⇒ |CF|=		|CB|
	3

c.n.w.