równoległobok geometria analityczna

równoległobok geometria analityczna mat: Punkty P = (−3, 4), Q = (2, 1) i R = (−1, −1) są środkami boków równoległoboku. Wyznacz współrzędne wierzchołków tego równoległoboku.

2 kwi 17:15

wmboczek: gdzie jest środek równoległoboku i jak się mają odcinki PQ, PR lub QR do przekątnej + wektory pewnie ze 3 warianty wyjdą, mi po pierwszym się znudziło

2 kwi 17:28

mat: nie rozumiem, dalej nie wiem jak to zrobić

2 kwi 17:34

mat: A odległość PQ to nie jest przypadkiem długość boku

2 kwi 17:35

wmboczek: z tw Talesa masz że PQ to pół przekątnej i || do niej środek jest pomiędzy PR Od środka +/− wektor PQ i będziesz miał 2 wierzchołki

2 kwi 17:39

mat: A nie jest tak że PQ to długość boku, a PR to połowa przekątnej

2 kwi 17:42

mat: lub OR to długośc boku a PQ pzekątnej

2 kwi 17:45

wmboczek: to są właśnie te 3 przypadki emotka

2 kwi 17:46

mat: aha chyba łapie, czyli długość boku to będzie 1−PQ 2−PR 3−QR i na podstawie tego policzyć tak

2 kwi 17:50

mat: MImo wszystko byłbym wdzięczny jakby ktoś to policzył dokładnie

2 kwi 17:54

wmboczek: właśnie

2 kwi 17:54

wmboczek: mogę podać jedno z rozw (1,7/2) (−5,−1/2) (3,−3/2) (−7,9/2)

2 kwi 17:55

mat: ale jak sobie narysuje to nie potrafię sobie wyobrazić by QR było długością boku ( były to środki naprzeciwległych boków), tak samo PR

2 kwi 17:56

mat: @wmboczek Długość boku PQ tak

2 kwi 17:57

wmboczek: PR bok

2 kwi 17:58

mat: Punkt nawet chyba by nie należał do tego rónoległoboku co podałeś, coś nie pasuje emotka

2 kwi 18:01

mat: *P

2 kwi 18:02

Janek191: rysunek

Prosta QR

	−2		2
y =		x + b =		x + b Q = ( 2,1)
	−3		3

	2		1
1 =		*2 + b ⇒ b = −
	3		3

	2		1
y =		x −
	3		3

Prosta równoległa do pr RQ i przechodząca przez P = ( −3,4)

	2
y =		x + b₁
	3

4 = − 2 + b₁ ⇒ b₁ = 6

	2
a : y =		x + 6
	3

K − środek RQ

	1
K = (		, 0)
	2

Prosta PK

	−4
y =		x + b₂
	3,5

	8
y = −		x + b₂
	7

	4		4
0 = −		+ b₂ ⇒ b₂ =
	7		7

	8		4
y = −		x +
	7		7

Prosta równoległa do pr PK przechodząca przez R =( − 1, −1)

	8
y = −		x + b₃
	7

	8		15
− 1 =		+ b₃ ⇒ b₃ = −
	7		7

	8		15
m : y = −		x −
	7		7

================= Prosta równoległa do pr m i przechodząca przez Q = ( 2,1)

	8
y = −		x + b₄
	7

	16		23
1 = −		+ b₄ ⇒ b₄ =
	7		7

	8		23
n : y = −		x +
	7		7

====================== Teraz rozwiązać układy: 1) a i m

	2
y =		x + 6
	3

	8		15
y = −		x −
	7		7

	1
A = ( −4		; 3)
	2

============= 2) a i n

	2
y =		x + 6
	3

	8		23
y = −		x +
	7		7

	1
B = (− 1		, 5)
	2

============= Q − jest środkiem BC oraz R − jest środkiem AD Można wyznaczyć punkty C i D,

	1
C = ( 5		, − 3)
	2

=============

	1
D = ( 2		, − 5)
	2

===============

2 kwi 18:19

Janek191: Dużo liczenia − może jest krótszy sposób emotka

2 kwi 18:23

Janek191: Wektory → RQ = → B = P + 0,5 RQ = → A = P − 0,5 RQ = → BQ = ... → C = B + 2 BQ = → D = A + 2 BQ =

2 kwi 18:27

mat: @Janek191 ale Ty zrobiłeś tylko 1 przypadek jeszcze trzeba 2 pozostałe tak

2 kwi 18:32

Janek191: Jakie dwa ? emotka

2 kwi 18:52

Janek191: Masz w odpowiedzi trzy czwórki punktów ?

2 kwi 18:54

mat: Nie widze chyba zmeczony jestem moglbys wypisac te trzy czworki, widze tylko 4 punkty

2 kwi 19:31

Janek191: Kto powiedział,że są inne przypadki ? emotka

2 kwi 19:50

mat: No a te co podal @wmboczek tez pasuja za 3 przypadki, a ty rozpatrzyles chyba tylko 1

2 kwi 21:34

Eta:

Prostszy sposób z wykorzystaniem wektorów emotka

1/ jak na rys → → S(−2;1,5) SQ=[4, −0,5] =PB=[x_B+3, y_B−4] ⇒ x_B+3=4 i y_B−4= −0,5 to B(1;1,5) x_C=2x_Q−x_B i y_C=2y_Q−y_B ⇒ C(3; −1,5) x_A= 2x_P−x_B i y_A=2y_P−y_B ⇒ A(−7;4,5) x_D=2x_R−x_C i y_D=2y_R−x_C ⇒ D(−5;−0,5) Takie odp. podał wmboczek pozostałe położenia punktów P, Q, R rozwiąż podobnie

2 kwi 23:32

Mila:

Punkty P = (−3, 4), Q = (2, 1) i R = (−1, −1) 1) Środek QR jest punktem przecięcia przekątnych QR^→=DA^→⇔QR^→||DA^→ QR^→=[−3,−2] P=(−3,4)→T_{[−1.5,−1]}⇒A=(−4.5,3) P=(−3,4)→T_[1.5,1]⇒D=(−1.5,5) DQ^→=[3.5,−4] D=(−1.5,5)→T_[7,−8]⇒C=(5.5,−3) C=(5.5,−3)→T_[−3,−2]⇒B=(2.5,−5)

2 kwi 23:35

Mila:

2) Środek PQ jest punktem przecięcia przekątnych równoległoboku P = (−3, 4), Q = (2, 1) i R = (−1, −1)

	1		5
O=(−		,		)
	2		2

PQ→=[5,−3] PQ→=AB^→

	5		3		5
R=(−1,−1)→T_[		,−		]⇒B=(1.5,−		]
	2		2		2

	5		3		7		1
R=(−1,−1)→T_[−		,		]⇒A=(−		,		)
	2		2		2		2

	1		7
BQ^→=[		,		]
	2		2

	5		9
Q=(2,1)→T_{[¹₂,⁷₂]}⇒C=(		,		)
	2		2

	7		1		5		15
A=(−		,		→T_BC→=[1,7]⇒D=(−		,		)
	2		2		2		2

2 kwi 23:35

mat: Ok, dziękuje, czyli teraz jako długość jednego boku będą PQ lub RQ. I ich środek jest zarazem środkiem tego równoległoboku. Chyba rozumiem, dziękuje

2 kwi 23:35

Mila:

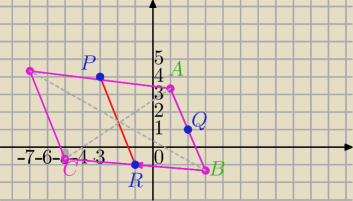
P = (−3, 4), Q = (2, 1) i R = (−1, −1) 3) środek PR jest punktem przecięcia przekątnych równoległoboku PR^→=[2,−5]=AB^→

	5		3
Q=(2,1)→T_[1,−		]⇒B=(3,−		)
	2		2

	5		7
Q=(2,1)→T_[−1,		]⇒A=(1,		)
	2		2

	1
BR^→=[−4,		]
	2

	1		1
R=(−1,−1)→T_[−4,		]⇒C=(−5,−
	2		2

D wyznacz sam.

2 kwi 23:36

mat: I Jeszcze jedna prośba do @Eta lub @Mila, spójrzcie na to zadanie jak powinno być rozwiązane : https://matematykaszkolna.pl/forum/321533.html Plis pomóżcie

2 kwi 23:38

Janek191: O, Mila się zlitowała i zrobiła mat: owi całe zadanie emotka

3 kwi 08:25