bardzo proszee o pomoc daniel: okresl dla jakich wartosci parametru m ∊ R rownanie : (x³ − m³)(x² −100 )(x² + 2mx +m² −9m) = 0 ma dokladnie 4 rozne pierwiastki rzeczywiste

Jerzy: ile już ma ?

daniel: x² − 100 czyli dwa , wiec pozostaje jeszcze jakies dwa , ale nie wiem jak potraktowac tamte nawiasy

daniel: ten ostatni gdybysmy wzieli delte > 0 to wychodzi na to ze delta w tym pierwszym nawiasie musi byc mniejsza od zera

daniel: a gdy w 1 nawiasie bedzie wieksza od zera to z kolei w ostatnim musi byc mniejsza i to da 4 pierwiastki te warunki wiec biore alternatywe?

daniel: tych dwoch przypadkow?

5-latek : x³−m³ rozpisz to sobie ze wzoru skroconego mnozenia a³−b³ ile bedzie pierwiastkow ?

daniel: (x−m)(x²− xm +m²) − 3 ?

Jerzy: Zauważ,że : x³ − m³ ma zawsze jeden pierwiastek, zatem ostatni nawias musi mieć tylko jeden i obydwa muszą być... ?

5-latek : Będzie tu jeden pierwiastek ale musisz zadbac o to żeby ile nie był rowny ? masz już 3 pierwiastki wiec Wiec ostatni czynnik ile musi mieć pierwiastkow ? Ale tez musisz zadbac o to żeby nie był rowny (−10) lub 10 bo maja być rozne

Jerzy: Cześć małolat .... x³ − m³ = 0 ⇔ x³ = m³ ⇔ x = m

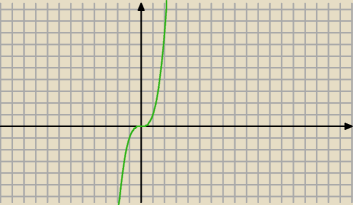
Jerzy: każda prosta równoległa do osi OX przecina wykres tylko w jednym punkcie

5-latek : Witaj Jerzy Spojrz na mój ostatni post

Jerzy: OK. .... ale nie ma potrzeby rozkładać tego na czynniki

5-latek : https://matematykaszkolna.pl/forum/321420.html chodzi o ten link

Jerzy: Nie gniewaj się.... ale nie mam dzisiaj siły, do analizy takich tasiemców

daniel: oo bardzo latwe zadanie jednak.. juz sie polapalem dzieki

5-latek : To tak jak ja dzisiaj (brak powera ) Jeśli możesz to sprawdz jutro OK?

daniel: nie... jest okeej wpisalem w mathematice i wolframie, dzialaa