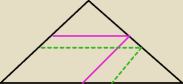
Możliwie największe pole rónoległoboku Majka: Proszę o pomoc. Z trójkąta ABC o podstawie AB = 30cm i ramionach AC=BC=20cm należy wyciąć równoległobok o największym polu. Oblicz długość boków równoległoboku, wiedząc, że jeden z kątów przy podstawie trójkąta jest jednocześnie kątem ostrym równoległoboku. Obliczyłam: H_Δ=75√7 próbowałam z stosunków boków, stosunek pól.. ale nic mi nie wychodzi..

===:

Majka:

H		h1
	=
x		x1

5√7		h1
	=
15		x1

	5√7x1
h1=
	15

	5√7x1
P▱=15*
	15

tak?

Majka:

	5√7x1
nieee... P▱=15*(5√7−		)
	15

Eta: https://matematykaszkolna.pl/forum/146670.html

Majka: ooo życie mi ratujesz dzięki

g:

1		1		1
	a*h =		(a−c)*h2 +		c*h1 + S
2		2		2

h2/h = (a−c)/a h1/h = c/a

1		1		1
	a*h =		(a−c)*h*(a−c)/a +		c*h*c/a + S | *a/h
2		2		2

S*a/h = −c² +ac Teraz trzeba znaleźć c maksymalizujące S (lub S*a/h co na to samo wychodzi). Równanie −c² +ac ma dwa pierwiastki (0,a), więc c maksymalizujące S to c = a/2. d z Talesa: d = b/2.

Eta: Za dużo tych literek ..... można dostać "oczopląsu"