pochodne. Jack: https://matematykaszkolna.pl/forum/320869.html zadanie 7... juz mi sie tak w glowie miesza, ze w koncu nwm co sie tam dzieje... wiem ze f '(x) = x

	−1
g ' (x) =
	x2

ale co z tego styczne sa prostopadle, czyli a₁ * a₂ = − 1 czyli co? x* (−1/x²) = − 1 ale te iksy chyba sa rozne... czy nie bo juz mi sie tak miesza, ze masakra

Jack: jesli to jest ok x* (−1/x²) = −1 wychodzi z tego ze x= 1 zatem y_f = 1/2 + a y_g = 1 czyli co, wystarczy porownac? 1/2+a = 1 ? a = 1/2? czyzby to bylo tak banalne?

Metis: Zapiszę rozwiązanie.

Krystian : Metis mam kilka pytań z jakich zbiorów uczysz się do maturki i kiedy zacząłeś się przygotować? (nie licząc normalnych lekcji matematyki w szkole)

Jack: Krystianie, "odpal" zbior z matmy ze strony cke...400 stron zadan i wszystko bedzie jasne

azeta: u Ciebie f'(x)*g'(x)=a₁*a₂? czym są a₁ i a₂, a czym są f'(x) i g'(x)?

Jack: f ' (od jakiegos punktu, a raczej iksowej) = a₁ g ' (od jakiejs iksowej) = a₂...

azeta: Dla jakiej wartości parametru a styczne do wykresów funkcji f i g w punkcie ich przecięcia są prostopadłe?

Jack: no wiec chodzi o punkt przeciecia wykresow, a nie stycznych.... czy odwrotnie?

azeta: szukasz takiego parametru a, dla którego te wykresy będą się przecinały i ponadto − w tym punkcie styczne do wykresów maja być prostopadłe.

Jack: duzo mi to nie mowi

Jack: Jak ktoe zechce to rozwiazac...to niech rozwiaze

Metis: Mam rozwiązanie Tylko ładnie zapiszę i wstawię linka.

Metis: Jednak nie jestem pewny. Masz odp. do tego ? a=−3/2 ?

Metis: Dobra, znalazłem błąd. Jutro wszystko ładnie Ci opiszę. a=0,5

Mila: W razie kłopotów piszcie, to napiszę.

kochanus_niepospolitus:

	1
f(x) =		x2 + a
	2

	1
g(x) =
	x

niech l oznacza rodzinę stycznych funkcji f(x) niech k oznacza rodzinę stycznych funkcji g(x) l: y − f(x₁) = f'(x₁)(x−x₁) k: y − g(x₂) = g'(x₂)(x−x₂) styczne będą prostopadłe jeżeli f'(x₁)*g'(x₂) = −1

	−1		x1
x1*		= −1 −>		= 1 −> x1 = x22
	x22		x22

	x22		x22
l: y −		− a = x22(x − x22) −> l: y = x22*x −		(2x22 − 1) + a
	2		2

	1		1		x		2
k:y −		= −		(x−x2) −> k: y = −		+
	x2		x22		x22		x2

I teraz: dla konkretnego parametr a będzie trzeba uzależnić od x₂ co będzie szalenie trudne

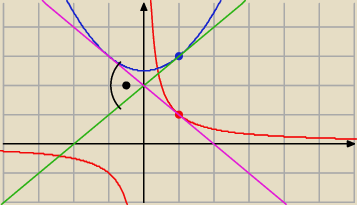
kochanus_niepospolitus: chyba, że zadanie nie zostało dokładnie napisane i należy przyjąć x₁=x₂ (wtedy oczywiście x₁ = x₂ = 1)

	5
Wtedy dosyć łatwo wyliczy się, że a=
	2

kochanus_niepospolitus: Jednak ogólnego wzoru na parametr a (dla dowolnego x₂ ∊ R) szczerze mówiąc nie jestem w stanie obecnie w łatwy sposób wyznaczyć.

kochanus_niepospolitus: dobra ... wracam do zadania ... zajarzyłem treść x₁ = x₂ ... ale dodatkowo g(x₁) = f(x₁) a więc z obliczeń napisanych o 00:18 wynika, że x₁ = x₂ = 1

	1		1		1
f(1) = g(1) −>		+ a =		⇔ a =
	2		1		2

Jack: matko jedyno, co sie tutaj stalo ;

Jack: czyli wychodzi tak jak mowilem? pochodna z pierwszego * pochodna z drugiego = − 1 wtedy x =1 1/2+a = 1 a = 1/2

Jack: czy to jest potrzebne co Kochanus obliczal?

Mila: Jack, co mam wyjaśnić? Napisz konkretnie.

Metis: U mnie się coś nie zgadza w rozwiązaniu i nie wstawiam Ale zadanko fajne.

Jack: Czy moge tak pisac jak pisze Pochodna z funkcji f a potem z funkcji g Wymnozyc pochodne i to sie rowna −1 Stad rozwiazanie x=1 Podstawic i zobaczyc jakie wyjda igreki w obu funkcjach Igrek w funkcjo f = 1/2 + a Igrek w funkcji g = 1 Skoro to ten sam punkt to y_f = y_g Zatem 1/2+a = 1 Stad a=1/2 Taka jest odpowiedz tylko nam czy tok myslenia nie jest bledny...

Jack: Zamiast "nam" powinno byc "nie wiem"

Mila:

	1
1) f(x)=		x2+a, f'(x)=x
	2

	1		1
g(x)=		, g'(x)=−
	x		x2

2) s_f: y=m*x+b styczna do wykresu funkcji f(x) s_g: y= k*x+c styczna do wykresu funkcji g(x) x₀ − pierwsza wsp. punktu przecięcia wykresów m=f'(x₀}⇔m=x₀

	1
k=g'(x0)⇔k=−
	x02

	−1
styczne są prostopadłe⇔m*k=−1⇔ x0*		=−1⇔
	x02

x₀=1

	1
f(1)=		+a
	2

g(1)=1

	1
wykresy przecinają się dla x=1⇔		+a=1
	2

	1
stąd a=
	2

	1		1
f(x)=		x+		,
	2		2

f(1)=1 ============ Wykresy i styczne: s_f: y=f'(1)*x+b⇔ y=1*x+b i 1=1*1+b, b=0 s_f: y=x s_g: y=−x+c i 1=−1+c, c=2 s_g: y=−x+2

Metis: Milu U siebie mam straszną kolizję oznaczeń. Dziękujemy

Mila: Dobranoc Do jutra.

Metis: Dobranoc Milu

Jack: Dziekuje