;))
Jack: Tez wam moge dac zadanka jeali chcecie

Poki co z z tematu wykorzystania pochodnych
26 mar 17:55
zef: O to możesz coś podrzucić chętnie się pouczę, a może coś nawet będę potrafił zrobić

26 mar 17:55
Jack:
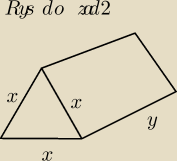
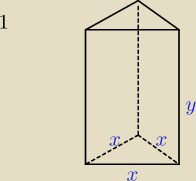
1. Objętość graniastosłupa prawidłowego trójkątnego jest równa 16. Jakie wymiary powinien mieć
ten graniastosłup, aby jego pole powierzchni całkowitej było najmniejsze?
2.Namiot ma kształt graniastosłupa prawidłowego trójkątnego (rys. na górze). Pole powierzchni
całkowitej namiotu (łącznie z podłogą) jest równe 18
√3. Dla jakiej długości krawędzi
x∊ <2;3>, objętość namiotu będzie największa?
3.Wyznacz współrzędne punktu P należącego do wykresu funkcji f i leżącego najbliżej prostej
x−y+2=0
a)f(x) = 1−x
2
4. Wyznacz dziedzinę funkcji f, określ jej najmniejszą wartość oraz naszkicuj wykres, jeśli :
f(x) = lim (1 + x
2 + x
4 + ... + x
2n)
n→
∞
5.* Funkcja f przyporządkowuje parametrowi p sumę sześcianów pierwiastków równania x
2 + px +
| | p | |
|
| = 0. Wyznacz dziedzinę i zbiór wartości funkcji f. |
| | 2 | |
| | x2+ax−4 | |
6.Punkt P(1, −2) należy do wykresu funkcji f(x) = |
| , b ≠ −1. Styczna do tego |
| | x+b | |
wykresu poprowadzona w punkcie P jest prostopadła do prostej 3x+y+5 =0. Oblicz a i b.
| | 1 | | 1 | |
7.Dane są funkcje f(x) = |
| x2 + a i g(x) = |
| . Dla jakiej wartości parametru a |
| | 2 | | x | |
styczne do wykresów funkcji f i g w punkcie ich przecięcia są prostopadłe?
| | 1 | |
8. Prosta o rónaniu y = |
| x jest styczna do wykresu funkcji : |
| | 4 | |
| | x2−x | | 1 | |
f(x) = |
| + cos 2α − |
| sin α w punkcie o dodatniej odciętej. Wyznacz α, jeśli |
| | 3x+1 | | 2 | |
α ∊<0;π>
Odpowiedzi zostana wrzucone pozniej ^^
26 mar 18:50
Jack: refreshuje bo zagina

27 mar 22:57
Metis: Kilka rozwiązałem, jutro wstawię .
27 mar 23:01
zef: Odświeżam, ktoś się podejmie rozwiązania, chciałbym się z tego trochę dowiedzieć

6 kwi 21:21
Jack: ja polowe rozwiazalem , ale nwm czy jest sens wrzucac

6 kwi 21:23
zef: Jak znajdę czas w weekend to sam popróbuję, coś może zrobię

6 kwi 21:24
zef: Zad.1
16=Pp*H
Pc=2Pp+Pb
Posłużę się tym rysunkiem.
Pc=8+3xy
I teraz liczyłbym pochodną dla zmiennej x i y i ekstrema, w taki sposób trzeba ?

6 kwi 21:31
zef: W objętości h zgubiłem :<
6 kwi 21:33
Jack: to jest liceum...
pochodna sie liczy
tylko po jednej zmiennej
oznaczmy krawedz jako x i wysokosc jako y
z tego co znamy wyznaczamy jedna zmienna np. wyznaczmy igrek
| | x2√3 | | x2√3 | |
Pc = 2PP + Pb = 2* |
| + 3*xy = |
| + 3xy |
| | 4 | | 4 | |
i teraz wstawiasz ten igrek do Pola i masz tylko jedna niewiadomo
potem pochodna, przyrownujesz do zera i ekstrema...
założenia oczywiscie
x,y > 0 (bo to dlugosci bokow)
| | 16*4 | |
skoro zrobilismy, ze y = |
| |
| | x2√3 | |
to
oczywiscie to jest spelnione...
6 kwi 21:38
zef: po podstawieniu y
√3x
3−512
√3=0
√3x
3=512
√3
x
3=512
x=8
16
√3+8
√3
24
√3
Dobrze ?

6 kwi 21:52
zef: dla x=8 pole będzie najmniejsze i będzie wynosiło 24√3
6 kwi 21:58
Jack:
oczywiscie w moim poscie 21:38 mam blad
jest napisane
| | x2√3 | |
Pc = 2Pp + Pb = 2 * |
| + 3xy |
| | 4 | |
| | x2√3 | |
a potem jest = |
| + 3xy (dwójka zaginęła) |
| | 4 | |
odp. jest 4, czyli sie zgadza bo 8/2 = 4
oczywiscie jak liczysz pochodna i przyrownasz do zera, to czy to jest minimum czy maximum
okreslasz poprzez rysunek krzywej.
wyszlo Ci x
3 = 512
x= 8 (wytlumacze na tym przykladzie)
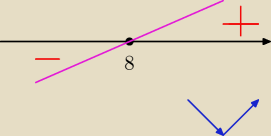
to zaznaczasz to miejsce zerowe i rysujesz zawsze od prawej do lewej, skoro to jest liniowa a
wspolczynnik jest dodatni, to od gory.
to co pod osia to robimy minus, to co ponad to +
i tlumaczy sie to tak
funkcja przyjmuje minimum dla x = 8 [f
min (8)]
to ze to jest minimum okreslasz po tym, ze jest najpierw minus a potem plus, a to z kolei
mozna wytlumaczyc tak, ze masz minus czyli idziesz w dol, a potem plus, czyli do gory, wiec
skoro szedles na sam dol a potem do gory, to musiales byc na samym wierzcholku dolu.
czyli jak bys szedl miedzy pagorkami (niebieski rysunek) dlatego minimum
6 kwi 22:17
Jack: oczywiscie w poleceniu pytali o wymiary...
wiec x = 4
y = ...
6 kwi 22:18
zef: No to można uznać że sobie poradziłem z tym zadaniem

Dzięki za szczegółowe objaśnienie
ekstremów, jutro postaram się jeszcze jakieś zadanie zrobić
6 kwi 22:21
6 kwi 22:23
Jack: 
6 kwi 22:26
6 kwi 22:34
Mila:
| x2√3 | |
| *y=16 /*4⇔x2√3y=64 /*√3 |
| 4 | |
| | x2√3 | |
P(x,y)=2* |
| +3*x*y , ⇔ |
| | 4 | |
| | x2*√3 | | 64√3 | |
P(x)= |
| +3*x* |
| |
| | 2 | | 3x2 | |
| | 64√3 | | 64 | |
P'(x)=x√3− |
| =√3*(x− |
| ) |
| | x2 | | x2 | |
| | 64 | | 64 | |
P'(x)=0⇔x− |
| =0⇔x= |
| ⇔x3=64⇔x=4 |
| | x2 | | x2 | |
P'(x)>0⇔x>4⇔dla x=4 funkcja P(x) ma wartość najmniejszą
P(4)=8
√3+16
√3=24
√3
6 kwi 22:58
Mila:
7 kwi 18:29
Jack: 
7 kwi 18:30
zef: Zad 2.
Pc=18
√3
x<2;3>
v=?
Pc=2Pp+3Pb
V=Pp*H
Z Pc wyznaczam y.
Liczę teraz pochodną z tego wyrażenia:
| | (36√3−x2√3)'*6x−(36√3−x2√3)*6 | |
y'= |
| |
| | 36x2 | |
| | (−2√3x)*6x−(36√3−x2√3)*6 | |
y'= |
| |
| | 36x2 | |
| | (−12√3x2)−(216√3−6x2√3) | |
y'= |
| |
| | 36x2 | |
| | −12√3x2−216√3+6x2√3 | |
y'= |
| |
| | 36x2 | |
Teraz pochodną przyrównuję do 0 aby znaleźć ekstrema.[(x∊<2;3>)]
−
√3x
2−36
√3=0
−
√3x
2=36
√3
−x
2=36
x
2=−36
No i wychodzi mi że pochodna nie ma miejsc zerowych :<
Ale to chyba nie koniec bo:
−x
2−36=0
(Oznacza parabolę skierowaną ramionami do dołu posiadającą wierzchołek który jest wartością
maksymalną)
Wierzchołek pokrywa się z osią Oy w punkcie −36
Rozpatruję to w przedziale <2;3> i wiem że większe będzie w 2 więc liczę f(2)
| | 32√3 | |
Odp: Największa objętość będzie wynosiła |
| |
| | 12 | |
Może mi ktoś to sprawdzić

7 kwi 21:09
zef:
7 kwi 21:31
Jack: do momentu
| | 36√3 − x2√3 | |
y = |
| jest ok |
| | 6x | |
potem niepotrzebnie liczysz pochodna
wyznaczyles sobie igrek po to, zeby wstawic do objetosci
liczysz pochodna od tego co ma byc najwieksze /najmniejsze. W poleceniu pytaja o najwieksza
objetosc. Dlatego jak masz juz igrek to go podstawiasz teraz do objetosci...tylko po to go
wyznaczales, bo bys mial dwie zmienne.
tutaj tamten igrek podstawiasz, wymnazasz i liczysz pochodna...
albo korzystasz ze wzoru na iloczyn w pochodnych...jak prosciej
wg mnie latwiej wymnozyc i uporzadkowac troche a potem pochodna
8 kwi 15:21
Jack: aj, zapomnialem sie zalogowac

8 kwi 15:22
zef:
Aj racja zapomniałem podstawić :<
Liczę pochodną z V
przyrównuję do 0
36−3x
2=0
3x
2=36
x
2=12
x=2
√3 lub −2
√3
Większa wartość będzie dla x=3
| | 32√3 | | 36√3−32√3 | |
f(3)= |
| * |
| |
| | 4 | | 6*3 | |
f(3)=10,125
Odp: Największa objętość będzie dla x=3 i będzie wynosiła 10,125

8 kwi 16:18
Jack: mam odpowiedz ze dla x=3, bo nie pytali ile bedzie wtedy wynosic objetosc, ale moge sprawdzic
rachunki
8 kwi 16:42
Jack: aczkolwiek nie rozumiem czemu skoro fmax wyszla dla x = 2√3
to w trojce jest najwieksza...
zazwyczaj wychodzi ze max jest tam gdzie chcemy... no ale trudno sie mowi
moze i git
8 kwi 16:56
azeta: bo chodzi o przedział <2,3>, taki haczyk 2
√3 nie należy do tego przedziału

też jeśli mogę coś poradzić odnośnie liczenia pochodnej: zauważ zef,
| | 36x−x3 | | 1 | |
V(x)= |
| = |
| (36x−x 3), a więc to zwykła pochodna z x n  żaden błąd oczywiście, |
| | 6 | | 6 | |
ale tam gdzie można wyłączyć stałą przed nawias, lepiej to zrobić.
8 kwi 17:20
zef: Dzięki za wskazówkę

Jutro postaram się zrobić jeszcze jakieś zadanko.
8 kwi 17:35
Jack: to powodzonka

8 kwi 19:07
 Poki co z z tematu wykorzystania pochodnych
Poki co z z tematu wykorzystania pochodnych

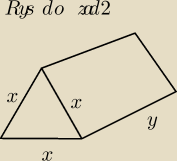 1. Objętość graniastosłupa prawidłowego trójkątnego jest równa 16. Jakie wymiary powinien mieć
ten graniastosłup, aby jego pole powierzchni całkowitej było najmniejsze?
2.Namiot ma kształt graniastosłupa prawidłowego trójkątnego (rys. na górze). Pole powierzchni
całkowitej namiotu (łącznie z podłogą) jest równe 18√3. Dla jakiej długości krawędzi
x∊ <2;3>, objętość namiotu będzie największa?
3.Wyznacz współrzędne punktu P należącego do wykresu funkcji f i leżącego najbliżej prostej
x−y+2=0
a)f(x) = 1−x2
1. Objętość graniastosłupa prawidłowego trójkątnego jest równa 16. Jakie wymiary powinien mieć
ten graniastosłup, aby jego pole powierzchni całkowitej było najmniejsze?
2.Namiot ma kształt graniastosłupa prawidłowego trójkątnego (rys. na górze). Pole powierzchni
całkowitej namiotu (łącznie z podłogą) jest równe 18√3. Dla jakiej długości krawędzi
x∊ <2;3>, objętość namiotu będzie największa?
3.Wyznacz współrzędne punktu P należącego do wykresu funkcji f i leżącego najbliżej prostej
x−y+2=0
a)f(x) = 1−x2






 oczywiscie w moim poscie 21:38 mam blad
jest napisane
oczywiscie w moim poscie 21:38 mam blad
jest napisane
 Dzięki za szczegółowe objaśnienie
ekstremów, jutro postaram się jeszcze jakieś zadanie zrobić
Dzięki za szczegółowe objaśnienie
ekstremów, jutro postaram się jeszcze jakieś zadanie zrobić





 Aj racja zapomniałem podstawić :<
Aj racja zapomniałem podstawić :<

 też jeśli mogę coś poradzić odnośnie liczenia pochodnej: zauważ zef,
też jeśli mogę coś poradzić odnośnie liczenia pochodnej: zauważ zef,
 żaden błąd oczywiście,
żaden błąd oczywiście, Jutro postaram się zrobić jeszcze jakieś zadanko.
Jutro postaram się zrobić jeszcze jakieś zadanko.
