ekstrema funkcji Jack: jesli mam jakakolwiek funkcje i mam wyznaczyc tylko ekstremum, bez monotonicznosci. To po policzeniu pochodnej i przyrownaniu jej do zera moge obliczyc druga pochodne od miejsc "zerowych" tej pierwszej i na podstawie czy jest dodatnia czy ujemna wskazac maximum albo minimum? 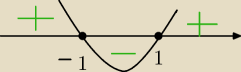Na lekcji wg pani powinnismy caly czas rozpisywac czyli po policzeniu pierwszej pochodnej przyrownujemy do zera potem rysujemy "wezyk" i sprawdzamy kiedy zmienia znak i stad odczytujemy(przy czym trzeba wszystkie przedzialy monotnicznosci rozpisac...) Wezmy sobie taka funkcje y = 2x³ − 6x − 4 f '(x) = 6x² − 6 6x² − 6 = 0 −>>> x² = 1 −−−> x = 1 lub x = − 1 1 i teraz metoda "szkolna" rysuje ten wezyk jak wyzej x ∊ (− ∞ ; − 1> f ' (x) > 0 funkcja rosnie x ∊ <− 1 ; 1> f ' (x) < 0 funkcja maleje x ∊ ( 1 ; ∞ > f ' (x) > 0 funkcja rosnie i dopiero teraz moge ekstrema ze f_max (−1) = ... f_min (1) = ... 2 A jakbym policzyl wtedy druga pochodna... f '(x) = 6x² − 6 −>> x = − 1 lub x = 2 Teraz druga pochodna f '' (x) = 12x f '' (−1) = − 12 <−−ekstremum lokalne max f '' (1) = 12 <−−ekstr. lok. min. Wychodzi dokladnie to samo bez zadnych przedzialow... Moje pytanie brzmi... czy moge jakos uzasadnic ze ta druga metoda jest dobra? Z tego co slyszalem to na studiach niektorzy wykladowcy tylko ta druga akceptuja... chociaz to tez zalezy od czlowieka

Eta: Dobra i 1 i 2

Jack: No ale na druga nauczyciel sie nie zgadza bo skad ma wiedziec czy sie znaki zmieniaja... jak moge to uzasadnic