Oblicz odległość między punktami. Ziqu: Punkt P należy do prostej o równaniu 2x + 3y − 4 = 0 i jest jednakowo odległy od punktów A=(1, −6) oraz B=(5, −2). Oblicz odległość punktu A od punktu P.

Jerzy: Znajdź punkt przeciècia symetralnej odcinka AB i danej prostej

Jack: punkt B nalezy do tej prostej...tak ma byc?

Ziqu: Liczę, ale coś źle mi wychodzi

Ziqu: @Jack Nie jest nic napisane, przepisałam polecenie dobrze

Jack: Szukasz prostej prostopadlej do prostej AB, przechodzacej przez srodek i szukasz przeciecia z prosta z polecenia.... Prosta AB ma wspolczynnik kierunkowy :

	yb − ya		−2 −(−6)		4
a =		=		=		= 1
	xb − xa		5−1		4

prosta prostopadla ma wspolczynnik a₁ = − 1

	1+5		−6 + (−2)
Srodek odcinka AB ma wspolrzedne (		,		)
	2		2

S_AB = (3, −4) wyznaczasz prosta ktora przechodzi przez ten punkt wiesz, ze a₁ = −1, oraz S_AB = (3, −4) zatem −4 = −1 *(3) + b −4 = −3 + b b = −1 zatem prosta prostopadla do AB przechodzaca przez srodek odcinka ma rownanie y = −x − 1 szukasz przeciecia z prosta 2x+ 3y −4 = 0, czyli 3y = 4 − 2x zatem nasza pierwsza prosta y = −x − 1 /// * 3 3y = −3x − 3 4−2x = −3x − 3 x = − 7 teraz y = −x − 1 = −(−7) − 1 =6 Punkt P ma wspolrzedne (−7,6)

Ziqu: Dziękuję

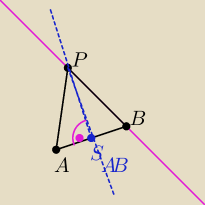
Jack: punkty stawiam przypadkowe, prosta tez, tylko zeby zilustrowac po co to wszystko robimy. ABP to nic innego jak trojkat skoro odleglosc AP jest taka sama jak BP, to na srodku pada wysokosc z punktu P, pod katem prostym... Odleglosc zawsze liczymy pod katem prostym wiec oto nam chodzilo mamy punkt P (−7,6) (jesli nie pomylilem obliczen). mamy obliczyc odleglosc tego punktu od punktu A (1, −6) no to odleglosc miedzy punktami liczymy ze wzoru https://matematykaszkolna.pl/strona/1248.html