Zadania dla [P[zef]] 5-latek : zef Wobec tego ze niedługo zdajesz mature to masz takie zadanka Zadanie nr 1

	a		b		a		b
Rozlozyc		−		na dwa czynniki których suma jest rowna		+		.
	b		a		b		a

Sprawdzic czy jest to jedyne rozwiązanie Zadanie nr 2 Rozwiaz równanie

	1		(3a−b)(a2+ab)−1		4		1
1+logx=		log[b−		]−		logb+		log(a3−ab2)
	3		b−2		3		3

zadanie nr 3 Oznaczajac przez S₁ sume n₁ wyrazow , przez S₂ sume n₂ wyrazow , przez S₃ sume n₃ wyrazow dowolnego ciągu arytmetycznego wykazac ze wówczas zachodzi

S1		S2		S3
	(n2−n3)+		(n3−n1)+		(n1−n2)=0
n1		n2		n3

Zadanie nr 4 Liczba a jest srednia arytmetyczna 3 liczb a liczba b jest serdnia arytmetyczna ich kwadratow Wyrazic za pomocą a i b srednia arytmetyczna trzech par iloczynow tych liczb Zadanie nr 5 Obwod rombu wynosi 2p a suma jego przekątnych m Znalezc pole rombu Zaadnie nr 6 Prosta rownolegla do podstawy trojkata którego pole jest rowne S odcia od niego trojkat o polu rownym q Wyznaczyc pole czworokąta którego trzy wierzchołki sa jednocześnie wierzchołkami mniejszsego trojkata a czwarty wierzchołek lezy na podstawie wiekszsego trojkata Zadanie nr 7 Do okręgu o promieniu R poprowadzona 4 styczne tworzące romb , którego wieksza przekatna jest rowna 4R Wyznaczyc pole każdej z figur ograniczonej dwiema stycznymi poprowadzonymi ze wspólnego punktu i lukiem okręgu zawartym miedzy punktami styczności Zadanie nr 8 Podstawa ostrosłupa jest wielokąt opisnay na okręgu o promieniu r Obwod wielokąta jest rowny 2p , a sciany boczne ostrosłupa sa nachylone do płaszczyzny podsatwy pod katem α. Znajdz objetosc ostrosłupa Zadanie nr 9 W ostrosłupie prawidłowym czworokątnym kąt dwuścienny przy podstawie jest rowny α Przez krawedz posdtawy rowna b poprowadzono plaszczyzne tworzaca z podstawa kat β. Znalezc pole powierzchni przekroju Zadanie nr 10 . Krawedz szsecianu jet rowna a, AB jest jego przekatna . Znalezc promien kuli stycznej do trzech scian schodzących się w wierzchołku A i jednocześnie stycznej do trzech krawędzi wychodzących z wierzchołka B . Zlaezc także pole powierzchni części kuli lezacej na zewnątrz szsescianu Zadanie nr 11 Sprawdzic tozsamosc 2(sin⁶x+cos⁶x)−3(sin⁴x+cos⁴x)+1=0 Zadanie nr 12 Rozwiaz równanie

	3π		π−x
2[1−sin(		−x)]= √3tg
	2		2

Mysle ze na razie Tobie to wystarczy

zef: Maturka to u mnie dopiero za rok To że zajmuję się pochodnymi itd. nie oznacza że jestem w klasie maturalnej Nie wiem czy poradzę sobie z którymś z tych zadań :<

5-latek : Probuj , dopytuj także innych uzytkownikow foru

Eta: zad5/ f+e=m i f²+e²=4a² i 2a=p

	fe		m2−p2
f2+e2= (f+e)2−2fe ⇒ m2−2fe= p2 /:4 ⇒		=P=
	2		4

dla m>p

5-latek : Dzien dobry Eta Pozdrawiam Życzę zdrowych i wesołych Swiat Wielkanocnych

Eta: Witaj "małolatku" Tobie też życzę zdrowych i spokojnych Świąt .

Eta: Ładne zadanka wrzuciłeś Zapoczątkowałam rozwiązaniem aby post nie "przepadł" i zobaczyli go maturzyści Rozwiązania pozostałych zostawiam już maturzystom ( ale coś się nie "palą"

zef: zad 4 1^o(z+x+c)/3=a z+x+c=3a 2^oz²+x²+c²/3=b zx+zc+xc=? 2^o (z+x+c)²−2zx−2zc−2xc=3b −2zx−2zc−2xc=3b−(z+x+c)² 2zx+2zc+2xc=(z+x+c)²−3b

	(z+x+c)2−3b
zx+zc+xc=
	2

	(3a)2−3b
zx+zc+xc=
	2

	9a2−3b
zx+zc+xc=
	2

Dobrze ?

zef:

9a2−3b
	teraz powinno być ok
6

zef: Przemnożyłem obie strony przez 1/3 na sam koniec

Eta: ok ...

Eta: Poprawny wynik w poście 17:03

zef: Hmm.. a nie powinienem wyznaczyć (ax+zc+xc)/3 ?

Eta:

	xc+zc+xz		3a2−b
Można zostawić :		=
	3		2

zef: 17:05 napisałem że mnożę obie strony przez 1/3

5-latek : Pokazalem tez Metisowi Może tez spojrzy . zef

	3a2−b
Odp to
	2

	zx+zc+xc
Masz policzyć
	3

Eta: Teraz "łap " zad. 6 (

zef: 5−latek Napisałem że mój ostateczny wynik z postu 17:03 mnożę obustronnie przez 1/3 bo dopiero pózniej zorientowałem się co mam wyznaczyć. Ostatecznie mi wyszło to co powinno

5-latek : Tak wiem ze napisales . Ja tez CI odpisałem i zamiast wyślij skasowałem swój post

zef: Nie wiem czy sobie jeszcze poradzę z którymś zadaniem chyba jeszcze nie mój poziom.

Eta: Dobrze, już się nie przechwalaj Licz następne , to wyślę Ci skrzynkę ..............

glax: zad.11 Sprawdzic tozsamosc 2(sin⁶x+cos⁶x)−3(sin⁴x+cos⁴x)+1=0 L=2[(sin²x+cos²x)³ − 3sin²xcos²x(sin²x+cos²x)] −3[(sin²x+cos²x)² −2sin²xcos²x]+1= =2 −6sin²xcos²x −3 +6sin²xcos²x +1=0 zatem L=P czyli taka tożsamość zachodzi

zef: Zad 7 Wyszły mi 2 odpowiedzi

4R2sinx−R2
4

lub

3R2sinx−R2
4

Czy coś z tego jest dobrze ? Jeśli nie to spróbuję w inny sposób

Godzio: zef, jeżeli w poleceniu nie było 'x' to nie powinieneś podać odpowiedzi z 'x'

5-latek : Wolalbym zebys zrobil rysunek do zadania i pokazal obliczenia Mam inne odpowiedzi do zadania . najwazniejszsy jest rysunek

zef: Ok chwila

glax: Zadanie nr 12 Rozwiaz równanie

	3π		π−x
2[1 −sin(		−x)]=√3tg
	2		2

	x
2[1 +cosx]=√3ctg
	2

i co dalej, dobrze mam do tego momentu?

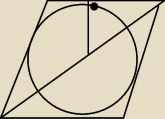
zef: Próbowałem to zrobić w taki sposób: e=4R a=? c=1/2 boku c²+R²=(2R)² c²=4R²−R² c²=3R² c=√3R więc bok wynosi 2√3R Pole tych obszarów które musimy wyliczyć

Prombu−Pokręgu
4

Zaczynam liczenie pola rombu: a²sinx=? (2√3R)²sinx 12r²*sinx I teraz wyznaczyłbym ten x: Przekątna jest dwusieczną i korzystam z tego małego trójkąta gdzie zaznaczyłem kąt prosty: 1/2x=z tgz=R/√3R tgz=1/√3 tgz=√3{3} z=30 stopni zatem 2z=x=60stopni Podstawiam:

Prombu−Pokręgu
4

12R2sin60−πR2
4

√3   12R2* −πR2   2
4

6√3R2−πR2
4

I to jest mój końcowy wynik

5-latek : Nie czytasz dokładnie polecenia masz wyznaczyć pole każdej z figur .....

zef:

6√3R2−πR2
	− pola dwóch figur przy których kąt pomiędzy stycznymi wynosi 60 stopni
2

12R2sin120o−πR2		6R2−πR2
	=		− pola dwóch figur przy których kąt pomiędzy stycznymi
2		2

wynosi 120 stopni

5-latek : zef A powiedz mi co ja mam z Twojego rysunku odczytac ? Jest po prostu niedbale zrobiony Już nie chodzi o jakość ale gdzie jakiekolwiek oznaczenia

glax: 17:42 jak dokończyć

	√3		x
1+cosx=		ctg
	2		2

5-latek : Widzisz dlaczego się czepiam tego ? Dlatego ze dawniej na maturze maturzysta musial zrobić sam rysunek do zadania . Nie tak jak teraz

zef:

	6√3R2−πR2
Według mnie każde pole wynosi
	4

A każde dlatego że kąty w tym rombie to 60,120,60,120 a sinus tych wartości wynosi tyle samo √3/2 Taka jest odpowiedź?

zef: Rysunek robiłem na kartce i był troszkę dokładniejszy

ZKS: Podpowiedź.

	x
1 + cos(x) = 2cos2(		)
	2

5-latek : Odpowiedz jest taka

	R2(3√3−π)
S1=
	3

	R2(2√3−π)
S2=
	6

zef: Hmm no byłem prawie pewny swojego wyniku, nie wiem gdzie mam błąd.

Eta: Podpowiedź może też być taka :

	x		1+cosx
ctg		=
	2		sinx

ZKS: Chyba nawet lepsza.

zef: Eta Mogłabyś zerknąć na moje rozwiązanie 17:43 ?

glax:

	x		√3	x   cos   2		x		x
2cos2(		)=			|* sinx		∧ |: cos
	2		2	x   sinx   2		2		2

	x		√3
sin		=
	2		2

	x		π		x		π
(		=		+2kπ ∨		=−		+2kπ) ∧ k∊ℤ
	2		6		2		6

	π		π
( x=		+4kπ ∨ x=−		+4kπ ) ∧ k∊ℤ
	3		3

ZKS: Już na samym początku 0 punktów za podzielenie przez coś co równa się zero.

glax: założenia trzeba co nie?

	x
cos		≠0 ⇔( x≠π +2kπ ∨ x≠ −π +2kπ) ∧ k∊ℤ
	2

	π		4π
i tam poprawka (x=		+4kπ ∨ x=		+4kπ) ∧ k∊ℤ
	3		3

glax:

	x
i sin		też założenie
	2

ZKS: Dziedzinę to się ustala przed jakimś przekształceniami.

Eta: @zef okrąg nie ma pola !

Jack: jak to nie , wszystko musi miec, nawet odcinek i prosta... DDDDDD

Metis: koło

5-latek : Dlatego caly czas prosze o w miare dokładny rysunek

zef: No okrąg nie ma pola ale ten okrąg potraktowałem jako koło bo interesuje mnie to co jest poza tym okręgiem Więc jak to liczyć

Eta:

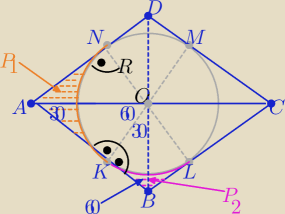
	√3
|AO|=2R , |AK|=|AN|=√3R , |KB|=|BL|=		R
	3

	1		R2		R2(3√3−π)
P1(AKN)= P(AKON)−		πR2= R2√3 −		π=
	3		3		3

	√3		1		R2(2√3−π)
P2(KBL)=		R2−		πR2=
	3		6		6

zef: Czytelny rysunek jednak daje bardzo dużo

Eta: W geometrii .... to 3/4 sukcesu

5-latek :

Eta: zad 6 odp: P₁=√Sq

zef: W tym 6 nie wiem jak narysować nawet :<

Eta: 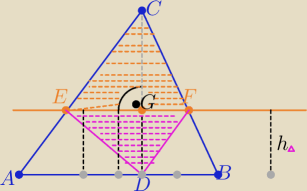zad.6 Z treści zadania P(EFC)= q i P(ABC)=S P₁=P(CEDF)= q+P(EDF) , P(EDF)=S₁ wartość pola S₁ nie zależy od położenia czwartego wierzchołka

	1
bo S1=		|EF|*h , EF|| AB
	2

zatem przyjmuję D ,który jest spodkiem wysokości CD trójkąta ABC ⇒CD⊥EF

	|EF|*ICD|		|EF|*|CG|		P1		|CD|
to P1=		i q=		⇒		=
	2		2		q		|CG|

	|CD|
z podobieństwa trójkątów ABC i EFC z cechy (kkk) w skali k=
	|CG|

S		S		|CD|
	=k2 ⇒		=(		)2
q		q		|CG|

	S		P12
zatem:		=		⇒ P12=Sq ⇒P1=√Sq
	q		q2

5-latek : Dobry wieczor Eta Chyba za trudne dla maturzystów bo rysunki należy robic

Eta: Dobry wieczór "małolatku"

5-latek : W zwiazku z tym ze masi maturzysci uporali sie szybko z tymi zadaniami to w najblizszym czasie przygotuje nowy zestaw zadan dla nich

zef: Może coś prostszego to i ja coś zrobię

Jack: https://matematykaszkolna.pl/forum/320869.html