46 pies: rozwiaz nierownosc : −x⁵+2x⁴+8x³−16x²−16x+32 probowalem pare razy ale nie wiem jak to pogrupowac

pies: acha tam ma byc ≥0

Smule: Nie musisz robić tego metodą grupowania

Smule: https://matematykaszkolna.pl/strona/121.html Na podstawie tego spróbuj znaleźć pierwiastki wymierne w dzielnikach liczby 32 i 1

Mila: x⁴*(−x+2)+8x²*(x−2)−16(x−2)=0 (x−2)*(−x⁴+8x²−16)=0⇔(x−2)*(−1)*(x⁴−8x²+16)=0⇔ (x−2)*(−1)*(x²−4)²=0 (x−2)*(−1)*(x−2)²*(x+2)²=0 Przechodzimy do nierówności: (x−2)*(−1)*(x−2)²*(x+2)²≥0⇔ (−1)*(x−2)³*(x+2)²≥0 x=2 pierwiastek potrójny x=−2 pierwiastek podwójny x≤2 =====

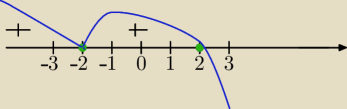
Jack: −x⁵ +2x⁴ + 8x³ − 16x² − 16x + 32 ≥ 0 −x⁴(x − 2) + 8x²(x−2) −16(x − 2) ≥ 0 (x−2)[−x⁴ + 8x² − 16] ≥ 0 Rozbijmy samo −x⁴ + 8x² − 16 =0 k = x² −k² + 8k − 16 =0 −(k−4)² = 0 k = x², więc −(x²−4)² = 0 −(x−2)²(x+2)² x = 2 lub x = − 2 wiec nasza nierownosc... (x−2)[−1(x−2)²(x+2)²] ≥ 0 −(x−2)³(x+2)² ≥ 0 /// * (−1) (x−2)³(x+2)² ≤ 0 rysujesz... i odczytujesz