Prawdopodobieństwo Metis: Milu , PW zerkniecie ? 1) Losujemy kolejno bez zwracania liczby ze zbioru {1,2,3,4,5,6,7}.Zapisane w kolejności tworzą ciąg 7− wyrazowy. Prawdopodobieństwo, że otrzymany ciąg będzie monotoniczny jest równe: Ciąg wylosowanych liczb będzie monotoniczny tylko wtedy gdy wylosujemy kolejno 1,2,3,4,5,6,7 lub 7,6,5,4,3,2,1 Czyli takich ciągów jest 2. Model : D_l − losowy wybór liczb ze zbioru 7 elementowego bez zwracania Taki wybór utożsamiamy z permutacjami, zatem: Moc Ω=7! A− zdarzenie polegające na ułożeniu ciągu 7 wyrazowego w taki sposób by był monotoniczny Moc A= 2 Na pods. kl. def. prawdopodobieństwa:

	2
P(A)=
	7!

Jest ? 2) Z urny zaw. 11 ponumerowanych kul losujemy 3 bez zwracania. Prawdopodobieństwo, że numery wszystkich wylosowanych kul będą nieparzyste wynosi . D__l− wybór 3 kul z 11 bez zwracania Moc Ω=11*10*9 //losujemy pierwsza − mamy 11 możliwości drugą już 10 trzecią 9 A− zdarzenie w którym numery wylosowanych kul są nieparzyste Czyli mamy do {1,3,5,7,9,11} I nie wiem jaka będzie moc zbioru A

olekturbo:

	11 3
Ω =

	6 3
A =

olekturbo: 1) ok

Saizou : w sumie zależy jak ponumerujesz kule np. {2,4,8,...,24} to P(A)=0 jeśli natomiast {1,3,5,..,21}, P(A)=1

Mila: 1) Dobrze. 2) Olek dobrze. Nie uwzględnia kolejności. 2) Sposób Metisa |Ω|=11*10*9 |A|=6*5*4

	6*5*4		4
P(A)=		=
	11*10*9		33

Uwzględnia kolejność.

Metis: Siemka Saizou olek źle podaje Ω. Mojej Ω jestem pewny w 2

Mila: 2) Warunek, że kule ponumerowane od 1 do 11.

Metis: Hmmm czyli różnią się na Ω ? W moim zapisie Ω = 990 U Olka Ω= 165

Metis: *Nam.

olekturbo: Ja nie uwzględniłem kolejności i zastosowałem kombinacje, natomiast ty przyjąłeś kolejność i zastosowałeś wariacje

Mila: Konsekwentnie, kombinacje w |Ω| i |A| albo wariacje bez powtórzeń w |Ω| i |A|. Oblicz P(A) w przypadku Olka.

Saizou : Witam wszystkich

Metis: Milu a możesz mi wyjaśnić skąd 6*5*4 ? Mam 6 kul. Losuje pierwsza na 6 moz. druga na 5 i czwartą na 4?

olekturbo: tak

olekturbo: trzecią na 4

Metis: No no

Aga1.: Kule można losować : −bez zwracania wylosować jedną , odłożyć ją na bok wylosować drugą, odłożyć ją i wylosować trzecią. −ze zwracaniem wylosować jedną, wylosowaną kulę zwrócić do urny, wylosować drugi raz kulę i wylosowaną wrzucić do urny i losować trzecią. Lub też trzy naraz tak jak zrobił Olek. Według mnie to sposób Metisa jest poprawny

Metis: Milu jesteś może? Mam jeszcze kilka zadanek do sprawdzenia i kilka wątpliwości.

Mila: Jestem.

Metis: 3) Rzucamy dwukrotnie kostką sześcienną. Oblicz prawdopodobieństwo wyrzucenia sumy oczek w obu rzutach równej 5 jeśli na pierwszej kostce wypadła 1. Na początku utożsamiłem to zadania z klas. definicją prawdopodobieństwa.

	1
I otrzymałem wynik		.
	6

(1,X) 1+X=5 Czyli X=4 Czyli zdarzeniu, że suma oczek bedzie równa 5 i pierwsza kostka pokaże 1 to 1 . Ω=36 Zatem P(A)=1/36 Ale zauważyłem , że treść tego zadania możemy zapisać: Rzucamy dwukrotnie kostką sześcienną. Oblicz prawdopodobieństwo wyrzucenia sumy oczek w obu rzutach równej 5 pod warunkiem, że na pierwszej kostce wypadła 1. I tutaj otrzymuję wynik 1/6. Korzystam ze wzoru na prawdo. warunkowe. Możesz mi wyjaśnić czemu te wyniki nie są jednakowo prawdopodobne?

Metis: Chodzi o to, że jesteśmy pewni że na pierwszej kostce będzie 1 , a o liczbie na kości drugiej zdecyduje los?

Mila: 1) W (1) sposobie obliczyłeś prawdopodobieństwo zdarzenia na pierwszej kostce wypadło 1 oczko i suma oczek jest równa 5. 2) Tu trzeba liczyć ze wzoru na prawd. warunkowe A− suma oczek jest równa 5. B− na pierwszej kostce wypadło 1 oczko. |B|=6 |A∩B|=1

	|A∩B|		1
P(A/B)=		=
	|B|		6

Mila: W zadaniu wiadomo, że na pierwszej kostce masz 1 oczko. Zatem nie musisz rozpatrywać wszystkich (36) możliwości ,tylko : Ω_B={(1,2),(1,3),(1,4),(1,5),(1,6)}

Metis: 4) Dany jest wielokąt wyp. o n wierzchołkach. Jakie jest prawdopodobieństwo, że dwa losowo połączone wierzchołki wyznaczają bok tego wielokąta. Nie wiem jak rozwiązać to zadanie. Jeżeli mamy n wierzchołków to z jednego wierzchołka możemy wyprowadzić (n−3) przekątnych czyli nie możemy połączyć dwóch sąsiednich wierzchołków ( bedą to boki) I zdarzeniem przeciwnym działac?

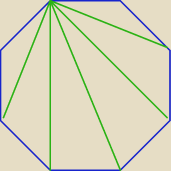
Mila: n=8 Liczba boków jest równa 8.

	n 2
Dwa wierzchołki możesz wylosować na :		sposoby,

tyle odcinków możesz utworzyć , część z nich to boki wielokąta, a część to przekątne

	n 2
|Ω|=

A− losowo wybrane wierzchołki są końcami boku wielokąta |A|=n

	n
P(A)=
	1   n*(n−1) 2

( liczba boków podzielona przez liczbę wszystkich utworzonych odcinków)

	2
P(A)=
	n−1

Dla n=8

	2
P(A)=
	7

Przy okazji oblicz, jakie jest prawd. że dwa losowo połączone wierzchołki wyznaczają przekątną tego ośmiokąta.

Metis: Rozumiem wszystko , szkoda, że sam na to nie wpadłem Muszę przerobić mnóstwo zadań z rachunku, aby to "złapać" , ale mam tak mało Jeżeli P(A) oznacza prawdopodobieństwo, że dwa wybrane wierzchołki są bokami . To zdarzenie przeciwne 0 dwa wybranie wierzchołki nie są bokami. Jeśli nie są bokami to są przekątnymi:

	2		n−1		2		n−3
1−		=		−		=
	n−1		n−1		n−1		n−1

Dla ośmiokąta: 5/7 No i rozsądek podpowiada, że jest bo wybór przekątnych jest bardziej prawdopodobny niż wybór boków.

Mila:

Yellow: Witam Przepraszam że tutaj pisze ,ale mam pytanie do Metis gdzie moge znalezc odpowiedzi do arkusza z zadaniami takimi jak w poscie https://matematykaszkolna.pl/forum/316079.html ?

Metis: Cześć To nie arkusz. Zadanka ze zbioru Omega.

Yellow: Aha, dzieki, ja mam te 3 zadania w arkuszu maturalnym z matematyki nr 5 arkusz probny poziom rozszerzony Officyna Edukacyjna ale nie mam odpowiedzi do tego zestawu i nie wiem jak sprawdzic

Metis: A wiesz co , może i to były arkusze Pazdro Muszę sprawdzić

Metis: Tak, to jednak arkusze Pazdro

Yellow: Masz może do niego odpowiedz ?

Yellow: do tego arkusza tylko

Metis: Mam

Yellow: A mozesz zrobic zdjecie i gdzies umiescic lub mi wyslać ?

Metis: GG masz?

Yellow: Kiedys mialem jakies 4 lata temu hasla ani loginu juz nie pamietam ale moge konto zalozyc

Metis: e−mail ? , cokolwiek

Yellow: odzyskalem konto GG:13135068

Metis: Do czego potrzebne odp. ?

Yellow: Do zadan od 1 do 18

Yellow: Arkusz ten co napisałem

Metis: Ale w jakim celu

Yellow: W celu sprawdzenia czy dobrz czy zle zrobilem zadania

Yellow: Co do niektorych mam pewnosc do innych nie

Metis: https://www.dropbox.com/sh/gdraaa8huqu5evm/AACN34aCCOUGJXpOXUHlWNFoa?dl=0

Yellow: Wielki dzięki a moge dostac jescze odp do 17 ?

Metis: Jest już w folderze.

Yellow: jeszcze raz wielkie dzięki , nie ma to jak sprawdzić zadania po 2 godzinnym ich rozwiazywaniu

Yellow: Mógłbys wysłać jeszcze raz to 17 bo przestalo dzialać, blad 404 ?

Metis: Wygasł link Przypomnij sie jutro .

Yellow: Ok,dzieki

Kacper: