matematykaszkolna.pl
Matura to bzdura Metis: Witajcie Możecie sprawdzić moje rozwiązanie? W odpowiedziach przedstawiony jest dowód nie wprost, ja wolę jednak tradycyjne metody emotka Zwróćcie uwagę na komentarze, są emotka czy trochę przesadzam ? Zadanie 1) Wykaż, że dla dowolnej liczby rzeczywistej a prawdziwa jest nierówność:
a2+3 
>2
√a2+2 
Moje rozwiązanie: http://i.imgur.com/XKHp92n.png
10 lut 22:09
Benny: Po co się tak męczyć Możesz sobie pomnożyć przez mianownik, podnieść do kwadratu i gotowe emotka
10 lut 22:14
Metis: Cześć Benny Teraz to widzę emotka Wydawałoby się, że to za proste.
10 lut 22:17
zombi: Metoda dowodzenia nie wprost, była używana już 300 lat p.n.e. więc nie wiem gdzie "nietradycyjność" tej metody
10 lut 22:18
Benny: No cześć emotka Te proste są najlepsze
10 lut 22:19
Metis: "tradycyjne"
10 lut 22:19
Mila: √a2+2>0 zatem możesz pomnożyć obie strony nierówności przez to wyrażenie. Trzeba dopisać komentarz, "w wyniku przekształceń równoważnych otrzymano nierówność prawdziwą dla ∀a∊R"
10 lut 22:20
Metis: Dziękuje Milu emotka Już dopisuje emotka
10 lut 22:21
Mila: Zamiast kwantyfikatora lepiej napisz "dla każdego a∊R". ( aby nie było nieporozumień)
10 lut 22:25
Jack: witam serdecznie
10 lut 22:27
Metis: Mam jeszcze takie zadanko, też proszę o sprawdzenie emotka Zadanie 2) Do wykresu funkcji f(x)=x3−3x−2 poprowadzono styczną k w punkcie M o odciętej x=−2. Prosta k przecięła wykres funkcji w punkcie A , gdzie A≠M. Podaj współrzędne punktu A. Moje rozwiązanie: 1: http://i.imgur.com/5bI6D60.png 2: http://i.imgur.com/laQRZau.png
10 lut 22:55
Mila: Wszystko dobrze, oprócz punktu wsp. A.
10 lut 23:08
Metis: Widzę emotka A=(4,50) . Źle odjąłem. Dziękuję emotka
10 lut 23:09
Mila: emotka
10 lut 23:10
piotr: styczna w −2 y=9x+14 A(4,50)
10 lut 23:16
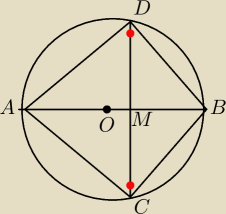
Metis: rysunekZadanie 3) W okręgu o środku O poprowadzono cięciwę CD , która przecięła średnicę AB w punkcie M, dzieląc je na odcinki AM i MB, gdzie |AM|=9, |MB|=4. Wiedząc, że punkt M jest środkiem cięciwy CD, oblicz pole ABCD. Trójkąty ABC i ABD oparte są na średnicy zatem kąt ACB i ADB są równe i mają po 90o. I teraz korzystam z własności, że: √9*4=|DM|=|MC| Stąd |DM|=|MC|=6
 1 
Pole trójkątów : 2* (
*13*6) to szukane pole czworokąta ABCD.
 2 
P=78j2 Wynik jest poprawny, ale zakładam, że |DM| i |CM| są wysokościami, jak to wykazać ? Ich równość wynika z faktu, że punkt M jest środkiem cięciwy CD.
10 lut 23:33
zombi: Kluczowe zdanie odnośnie twojego pytania Punkt M jest środkiem cięciwy
10 lut 23:36
Metis: Chciałem interpretować to z twierdzeniem o odległości punktu od prostej, ale nie wiem
10 lut 23:39
Metis: Potrzebuję w końcu tylko dowodu, że tam powstaje kąt prosty.
10 lut 23:41
zombi: Zauważ, że punkt M i O−środek okręgu wyznaczają nam jednoznacznie średnicę, czyli nasza średnica dzieli cięciwy na dwie równe części, a to jest własność symetralnej odcinka.
10 lut 23:42
zombi: Cięciwę*
10 lut 23:44
Metis: O Dzięki zombi, wszystko jasne emotka Nie widziałem tutaj symetralnej. Nieźle, że to wszystko jeszcze pamiętasz emotka
10 lut 23:45
zombi: 2. Sposób: Nasza cięciwa, ma swój początek i koniec na okręgu (oczywiste), dajmy na w punktach E i F. Jak spojrzysz na trójkąty OME i OMF są przystające na podstawie cechy BBB. Dlatego kąty OME i OMF są równe, czyli mają po 90o
10 lut 23:49
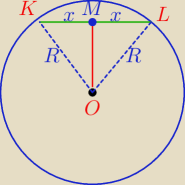
Mila: rysunek M≠O Odcinek łączący środek okręgu O ze środkiem cięciwy jest prostopadły do cięciwy ( jak napisał zombi)
10 lut 23:53
Metis: Dziękuje Wam emotka ciąg dalszy nastąpi jutro. Tymczasem Dobrej Nocy emotka
10 lut 23:59