Wyznaczanie argumentów pod koniec równania trygonometrycznego. Zwarty: Wyznaczanie argumentów pod koniec równania trygonometrycznego. Mam tylko malutkie pytanie, odnośnie wyznaczania końcowych wartości argumentów x w równaniach trygonometrycznych. Mam takie przykłady:

	1		1		3π		π
cosx = −		v cosx =		v cosx = −1 x∊( −		, −		)
	2		2		2		2

Jak wyznaczyć końcowe argumenty?

5-latek : Cosinus jest ujemny w 2 i 3 cwiatce i okres 2π dodatni jest w 1 i 4 cwairtce i tez okres 2π

Zwarty: dalej nie wiem jak rozwiązać, możesz jakoś jaśniej objaśnić?

5-latek : https://matematykaszkolna.pl/strona/1578.html tutaj lepiej będziesz miał objaśnione

Metis: Rozwiązujesz wszystkie równania . Później za k podstawiasz kolejne to liczby całkowite i sprawdzasz kiedy zawierają się w podanym przedziale. Ale ograniczasz i liczysz k.

	3π		π
−		<x<−
	2		2

Zwarty: cosx = 1/2 ⇔ x = π/3 + 2kπ cosx = −1/2 ⇔ x = −π/3 + 2kπ − dobrze rozumuję? jak potem uwzględnić przedział? po prostu podstawiając za k liczby całkowite? ujemne k także? może ktoś rozwiązać po prostu cosx = −1/2 po kolei? z góry dziękuję za pomoc

Zwarty: Pomoże ktoś?

Aga1.:

	1
cosx=
	2

	π		π
x=		+2kπ lub x=−		+2kπ, k∊C
	3		3

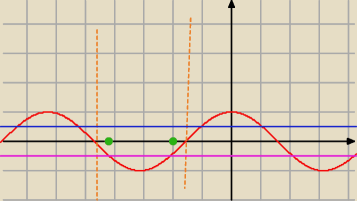
Jak widać równanie w tym przedziale nie ma rozwiązań

	1
A równanie cosx=−
	2

	2		2
x=		π+2kπ lub x=−		π+2kπ
	3		3

w podanym przedziale ma 2 rozwiązania

	2
k=−1 k=0 x=−		π
	3

	2		4
x=		π−2π=−		π
	3		3