kąt dwuscienny 123: Dane są dwa przystajace rownolegloboki ABCD i DCEF o wspolnym boku DC. Miara kąta ostrego obu rownoleglobokokow jest równa <CDA = <EDC = 30 stopni. Płaszczyzny zawierające te rownolegloboki tworzą kąt dwuscienny o mierze 60 stopni. Wiedzac, ze AD=DF=2, oblicz odległość między prostymi AB i EF. Nie wiem jak to zrobic i przyznam, że mam problem już z samym rysunkiem ktos pomoże?

123: ?

Ajtek: Na moje oko, coś nie tak jest z treścią zadania. Mamy kąt EDC i odcinek DF.

123: to zadanie 6.31 ze zbioru Kurczaba dla klasy trzeciej i przepisane jest słowo w słowo. a jak naszkicować rysunek chociaż?

===: Albo TY nie przykładasz znaczenia do tego w jakiej kolejności piszesz wierzchołki albo błąd w książce. Zadanie jest banalne ... ale źle opisane.

123: widocznie nie jest banalne skoro na podstawie treści też nie wiesz jak zrobić, bo zadanie jest przepisane dokładnie słowo w słowo

123: https://matematykaszkolna.pl/forum/234589.html <− tu jest zresztą to samo także przepisałem je dobrze

===: Zapytam Cię wprost ... piłeś coś czy jesteś głąb Popatrz na znaczenia wierzchołków i nie pieprz głupot

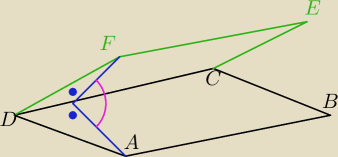
===: ... i popatrz czy kąt EDC jest kątem ostrym rónoległoboku

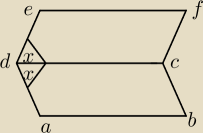
123: rysunek na szybko: CDA = EDC = 30 stopni = x o co chodzi Ci z tymi wierzchołkami?

123: rysunek robi się pod oznaczenia w zadaniu, więc twój jest po prostu zły, bo w ten sposób nie masz kąta równoległoboku, więc nie do zadania miej pretensje, a do swojego rysunku

===: TY NIGDY NIC SIĘ NIE NAUCZYSZ ! 1) Opisywanie wierzchołków ma swoje zasady 2) Naciągać pod oznaczenia to ty możesz ... 3) To jak sie to ma do dalszej treścI "AD=DF=2"

123: tylko z trzecim się zgodzę