Zdarzenia niezależne Metis: Rachunek prawdopodobieństwa... Co oznacza sformułowanie, że zdarzenia są niezależne? W podręczniku podana jest sucha definicja i warunek... W zadaniach pytają wprost o sprawdzenie czy zdarzenia są niezależne, a co to dokładnie oznacza? Istnieje dokładna definicja?

Tadeusz: http://www.naukowiec.org/wiedza/matematyka/zdarzenia-niezalezne_831.html

Tadeusz: https://matematykaszkolna.pl/strona/1021.html

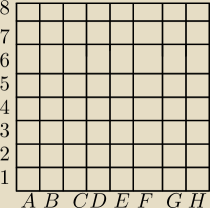
Jack: Zdarzenia A,B ⊂ Ω nazywamy niezaleznymi, jesli P(A∩B) = P(A) * P(B). Intuicyjnie zdarzenia okreslamy jako niezalezne, jesli nie maja one wzajemnie na siebie wplywu. O zdarzeniach,ktore nie sa niezalezny, mowimy ze sa zalezne <−− definicja z mojej ksiazki... Przyklad : Na jednym z 64 pol szachowych ustawiamy losowo wieze. Rozpatrzmy zdarzenia : A − wieza zostala ustawiona w wierszu 1,2 lub 3 B − wieza zostala ustawiona w kolumnie G lub H

	24		3
Zatem: P(a) =		=
	64		8

	16		1
P(b) =		=
	64		4

Zdarzeniu A∩B sprzyja szesc zdarzen elementarnych : G1, G2, G3, H1, H2, H3

	6		3
P(A∩B) =		=
	64		32

	3		1		3
Zauwazmy, ze P(A) * P(b) =		*		=		, zatem P(A∩B) = P(A) * P(B), co oznacza
	8		4		32

ze zdarzenia A i B sa niezalezne.

Jack: to ze dzisiaj piatek nie znaczy ze nie moze padac deszcz

PW: Niezależność ma swoją definicję i tyle. Zapisana w tej formie ma mało intuicyjny charakter, na ogół trudno niezależność zobaczyć na pierwszy rzut oka. Lepiej sobie uzmysłowić w ten sposób: Prawdopodobieństwo warunkowe zajścia zdarzenia A pod warunkiem, że miało miejsce zdarzenie B jest zdefiniowane wzorem:

	P(A∩B)
P(A|B) =		.
	P(B)

Jeżeli zdarzenia są niezależne, to wzór ten przyjmuje postać

	P(A)·P(B)
P(A|B) =
	P(B)

P(A|B) = P(A) − teraz może bardziej widać o co idzie. Prawdopodobieństwo zdarzenia A nie zależy od tego, czy zaszło zdarzenie B.

Mila: Zadania dla Metisa, Jack'a, Olka. 1) Rzucamy dwiema jednorodnymi kostkami do gry. Niech A oznacza zdarzenie polegające na wyrzuceniu 1 na pierwszej kostce, a B zdarzenie polegające na wyrzuceniu 2 na drugiej kostce. Czy zdarzenia A i B są niezależne? 2) Rozważamy trzykrotny rzut monetą symetryczną. Niech A oznacza zdarzenie polegające na otrzymaniu reszki w pierwszym lub drugim rzucie, zaś B zdarzenie polegające na otrzymaniu reszki w drugim rzucie lub trzecim rzucie. Czy zdarzenia A i B są niezależne? 3) Z talii 52 kart losujemy jedną. Niech A oznacza zdarzenie polegające na wylosowaniu asa, a B zdarzenie polegające na wylosowaniu kiera. Czy zdarzenia A i B są niezależne?

Metis: Witajcie Dziękuje Wam , za Wasz komentarz, przeczytałem i wiele mi się rozjaśniło. Milu Dziękuje za zadanka. Za chwilkę się za nie zabieram

Metis: Jack, Olek nie zamieszczajcie rozwiązań dopóki wszyscy nie zrobimy zadań, albo umieszczajcie je w postaci linków

olekturbo: 1) Ω = 36 A = {11,12,13,14,15,16} B = {12,22,32,42,52,62}

	1
P(AnB) =
	36

	6		6		1
P(A) * P(B) =		*		=
	36		36		36

Zdarzenia są niezależne

olekturbo: Sorry nie przeczytałem postu wyżej

olekturbo: Będę jutro Ide grać w karty. Powodzenia z zadankami

Mila: (1) dobrze.

olekturbo: 2) Rozważamy trzykrotny rzut monetą symetryczną. Niech A oznacza zdarzenie polegające na otrzymaniu reszki w pierwszym lub drugim rzucie, zaś B zdarzenie polegające na otrzymaniu reszki w drugim rzucie lub trzecim rzucie. Czy zdarzenia A i B są niezależne? Ω = 2³ = 8 A = {RRR,RRO,ROR,ORO,ORR,ROO} |A| = 6

	6
P(A) =
	8

B = {RRR,RRO,ROR,ORR,OOR,ORO} |B| = 6

	6
P(B) =
	8

AnB = {RRR,RRO,ROR,ORO,ORR}

	5
P(AnB) =
	8

	36
P(A) * P(B) =
	64

	5
P(AnB) =
	8

Zdarzenia nie są niezależne. Czy jest jakiś inny sposób na wyliczenie 'orłów' i 'reszek' niż ich wypisywanie?

olekturbo: 3) Z talii 52 kart losujemy jedną. Niech A oznacza zdarzenie polegające na wylosowaniu asa, a B zdarzenie polegające na wylosowaniu kiera. Czy zdarzenia A i B są niezależne? Ω = 52 A = 4 B = 13 P(AnB) = 1

	4		1
P(A) * P(B) =		* {13}{52} =
	52		52

	1
P(AnB) =
	52

Zdarzenia są niezależne.

Mila: Tu lepiej wypisać.

Mila: (1,2,3) dobrze.

olekturbo: Milu, dobrze? I czy mogłabyś odp na pytanie z 20:26 bo ja zawsze wypisuje wszystkie możliwe sposoby a nie znam "triku" na obliczenie np 3 reszek w 5 rzutach

olekturbo: Dzięki

Jack: Metis: "Jack, Olek nie zamieszczajcie rozwiązań dopóki wszyscy nie zrobimy zadań, albo umieszczajcie je w postaci linków" tiaa...czytanie ze zrozumieniem

Mila: Dokładnie 3 reszki w pięciu rzutach:

	5!
(RRROO)		permutacje z powtórzeniami
	2!*3!

Albo

5 3
	wybierasz 3 miejsca dla reszek, na pozostałe miejsca "wchodzą" orły.

Metis: Zobaczyłem rozwiązanie, więc szkoda mi przepisywać W twoim rozwiązaniu jak dla mnie brakuje modelu matematycznego, który w takich zadankach jest najważniejszy. 1) D_l − rzut dwiema kostkami sześciennymi Ω={(a,b), a, b∊{1,2,3,4,5,6}} Moc Ω =6²=36 A −zdarzenie polegające na wyrzuceniu 1 na pierwszej kostce. B− zdarzenie polegające na wyrzuceniu 2 na drugiej kostce. itd...

olekturbo:

Mila: Metis, zrozumiałeś niezależność zdarzeń?

Metis: Tak Milu Kojarzysz może pozycję: T. Sródka, T. Gerstenkorn Kombinatoryka i rachunek prawdopodobieństwa PWN ?

Mila: Jak najbardziej, z tego się uczyłam na studiach.

Metis: Teraz nie mam czasu na analizę takich książek Ale jeśli się uda − to po maturze będę miał dużo czasu

Saizou : ja na Rachunku miałem książkę Jacek Jakubowski, Rafał Sztencel,"Rachunek prawdopodobieństwa dla (prawie) każdego", Wyd. Srcipt

Metis: Siemka Saizou Jak leci?

Saizou : Cześć, a jakoś, nie lubię algebry No ale muszę się z nią teraz borykać. No i nie matematyczna część matematyki: statystyka A tak to już jest oki. Szkoda że mi się analiza skończyła, ale są równania różniczkowe Poza tym w życiu osobistym też jest spoko. A u Ciebie Metis?

Metis: Dasz radę jesteś "łebski" U mnie trwają przygotowania do matury Ale przydałby mi się jeszcze jeden rok. I na życie osobiste ja też na razie nie mam powodow do narzekania− ale to logiczne

Eta: http://zamosc.lscdn.pl/oz/aktualnosci/7647,039Lubelska-Proba-przed-Matura039-z-matematyki-Edycja-201516.html

Metis: O, dziękuję Eta ! Z tego co widzę R nie takie trudne.

Eta: