wielomian sylwester:

	3 2		5 3
Liczby		i		są pierwiastkami wielomianu W(x)=x3 +ax2+17x+b

a) wyznacz a i b b) znajdz trzeci pierwiastek wielomianu

	6+aIx−1I
c) rozwiąz nierówność		≥0
	bx−15

.: git majonez

jo: a) wstawić pierwiastki do wielomianu i przyrównać do 0: W(x₁)=...=0 i W(x₂)=...=0 i tym samym powstał układ równań z niewiadomymi a i b, który trzeba rozwiązać; b) podzielić trzeba wielomian przez (x−x₁) lub (x−x₂) i wyjdzie jakiś wielomian z którego będzie łatwiej znaleźć pierwiastki pozostałe; c) a tutaj to może później...

sylwester: pozniej wstawie moje rozwiazania

sylwester: a) a=−12 b=30 b) trzeci pierwiastek to 1 i jak

sylwester: jo czy możesz to sprawdzic

Bogdan:

3 2		5 3		5 2
	= 3,		=		= 10

x₁ = 3, x₂ = 10, x₃ = c W(x) = (x−3)(x−10)(x−c) = (x² − 13x + 30)(x − c) = x³ − cx² − 13x² + 13cx + 30x − 30c = = x³ + (−c − 13)x² + (13c + 30)x − 30c i W(x) = x³ + ax² + 17x + b 17 = 13c + 30 ⇒ 13c = −13 ⇒ c = −1 a = −c − 13 = 1 − 13 = −12 b = −30c = 30 Odp.: a = −12, b = 30, x₃ = −1 W(x) = x³ − 12x² + 17x + 30

sylwester: mhm dziekue a podpunkt c z nierównoscia wlasnie nie za bardzo to rozumiem

Anna: zrobię c)

Bogdan: Wstaw obliczone a, b, uprość i rozwiąż podobnie jak w zadaniu 31872

Anna:

	6 −12Ix−1I
		≥0
	30x−15

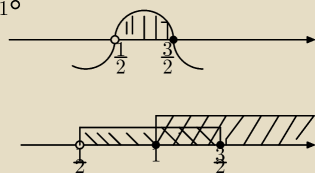
	2 − 4Ix−1I		1
		≥ 0 Zał. 10x−5 ≠0 ⇒ x ≠
	10x − 5		2

1⁰ x−1 ≥ 0 ⇒ x ≥1

	2−4(x−1)
		≥ 0
	10x−5

	2−4x+4
		≥ 0
	1ox−5

(6−4x)(10x−5) ≥ 0 2*5(3−2x)(2x−1) ≥ 0 I I

	1		1		1		1
x=1		x=		Na podst. wykresu: x∊ (		, 1		>
	2		2		2		2

Po uwzględnieniu warunku 1⁰ ( rys. na osi) mamy odp. 1⁰:

	1
x∊<1, 1		>
	2

2⁰ x−1 < 0 ⇒ x < 1

	2−4(−x+1)
		≥ 0
	10x−5

	2+4x−4
		≥ 0
	10x−5

(4x−2)(10x−5) ≥ 0 2*5(2x−1)(2x−1) ≥ 0 10(2x−1)² ≥ 0 I

	1
x=
	2

c.d. posyłam oddzielnie (rysunki się nie mieszczą)

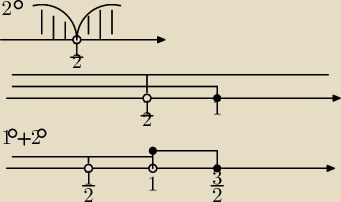
Anna: c.d. 2⁰.

	1
Z wykresu : x ∊ R \ {		}
	2

Po uwzględnieniu war. 2⁰ ( rysunek na osi) mamy odp. 2⁰ :

	1		1
x ∊ (−∞,		) ∪ (		, 1)
	2		2

1⁰ ∪ 2⁰ :

	1		1		1
Odp. x ∊ (−∞,		) ∪ (		, 1		>
	2		2		2