rozwiąż sylwester:

	I x−2I
Rozwiąż nierówność		≥2
	2x+6

sylwester: pomocy

Godzio: 1^o x∊(−∞,2)

−x+2
	≥2 /*(2x+6)2
2x+6

−(2x+6)(x−2) ≥ 2(2x+6)² −(2x² −4x +6x −12) ≥ 2(4x² + 24x + 36) −2x² −2x +12 ≥ 8x² + 48x +72 0≥10x² +50x +60 /:10 0≥x² + 5x + 6 Δ=25 − 24 = 1

	−5−1
x1=		= −3
	2

	−5+1
x2=		= −2
	2

x∊(−∞,−3) ∪ (−2,∞) biorąc pod uwagę nasz przedział => x∊(−∞,−3) ∪ (−2,2) 2^o x∊<2,∞) spróbuj dokńczyć biorąc pod uwagę przedział

Julek: Można szybciej niż rozpatrywanie przypadków

|x−2|
	≥2 / (2x+6)2
2x+6

|x−2|(2x+6)≥2(2x+6)² (x−2)(2x+6)≥2(2x+6)² ∨ (x−2)(2x+6)≤ −2(2x+6)² 2x² + 6x−4x−12 ≥ 8x² + 48x + 72 ∨ 2x² + 6x − 4x − 12 ≤ −8x² − 48x − 72 0 ≥ 6x² + 46x + 84 / 2 ∨ 10x² + 50x + 60 ≤ 0 / 10 0 ≥ 3x² + 23x + 42 ∨ x² + 5x + 6 ≤ 0 Δ₁= 529 − 504 = 25 Δ₂= 25−24 = 1 ...

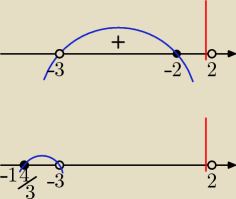
Bogdan: Można bez Δ. Założenie: x ≠ −3

|x − 2|		|x − 2|		|x − 2| − 4x − 12
	≥ 2 ⇒		− 2 ≥ 0 ⇒		≥ 0
2x + 6		2x + 6		2x + 6

	−x + 2 − 4x − 12
Dla x < 2:		≥ 0 ⇔ −5*2(x + 2)(x + 3) ≥ 0 ⇒ x ∊ (−3, −2>
	2(x + 3)

	x − 2 − 4x − 12		14
Dla x ≥ 2:		≥ 0 ⇔ −3*2(x +		)(x + 3) ≥ 0 sprzeczność
	2(x + 3)		3

Odp.: x ∊ (−3, −2>

sylwester: dzieki wielkie musze to jeszcze przeanalizowac

sylwester: nie rozumiem dlaczego jeżeli współczynniki przy x² sa dodatnie to ramiona paraboli sa skierowane do dołu? czy nie powinny być do góry?

sylwester: czy ktoś mogłby odpowiedziec na moje pytanie? proszę

sylwester: do góry

Nikka: w rozwiązaniu Bogdana ramiona paraboli są skierowane w dół bo przed nawiasami masz −10 i −6 czyli współczynniki przed x² są ujemne... a jak współczynnik przed x² dodatni to ramiona paraboli do góry...

sylwester: mhm juz rozumiem dziekuje zle spojrzalam