objętość ostrosłupa
Majka: w ostrosłupie prawidłowym czworokątnym o krawedzi podstawy równej 8cm krawedz boczna tworzy z
płaszczyzną podstawy kąt 60 stopni. oblicz objętość ostrosłupa
29 gru 12:32
kamil: pomagam
29 gru 12:40
Majka: ok

29 gru 12:40
mathalius:
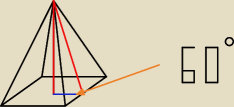
Długośc niebieska wynosi 4
Z sin60 wyliczamy wysokosc"
sin60=H/4
\tfrac{\sqrt{3}}{2} =H/4
H=2
√3
V=1/3*64*2
√3=128
√3/3 cm
3
29 gru 12:42
R.W.16l:
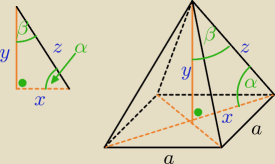
a=8cm
α=60 stopni
y=H
a
√2=8
√2
x=4
√2
β=30 stopni, czyli
y=x
√3 = 4
√6
z=2x = 8
√2, ale to nie ważne
H=y = 4
√6 (cm)
Pp=64 (cm
2)
Nie powinno być błędu
29 gru 12:43
mathalius: *\tfrac{\sqrt{3}}{2} tutaj ma być √3/2
29 gru 12:43
R.W.16l: trochę inaczej, weź przeanalizuj moje, proszę
29 gru 12:44
kamil: zajrzyj na stronke
995
V=Pp*H
podsawa jest kwadrat o znanej dl krawedzi wiec z Pp nie bedziesz miala problemu
moj sposob na obliczenie H jest taki;
wysokosc osrtoslupa (H) tworzy wraz z krawedzia boczna ostroslupa i polowa przekatnej podstawy
trojkat prostokatny, w ktorym znasz jeden kat(miedzy krawedzia boczna a polowa dlugosci
przekatnej podstawy) oraz dl polowy przekatnej podstawy. wyznaczasz sobie cos tego trojkata i
gotowe
29 gru 12:45
kamil: mathalius zle oznaczyles kat 60 stopni
29 gru 12:46
kamil: u mnie zamiast wyznaczac cos wyznacz tg
29 gru 12:48
R.W.16l: | | Pp*H | |
V=Pp*h, jeśli to graniastosłup, a to ostrosłup, więc V= |
| |
| | 3 | |
29 gru 12:48
kamil: no faktycznie.
29 gru 12:55
domi: W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość √2 , a krawędź
boczna 3 cm. Wysokość tego ostrosłupa jest równa
24 wrz 16:00
Eta:
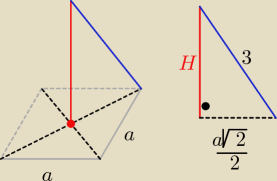
a=
√2 , H >0
z tw. Pitagorasa H
2= 3
2−1
2 ⇒ H=.........
24 wrz 16:06
ola: W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość √2 , a krawędź boczna √3 cm.
Wysokość tego ostrosłupa jest równa
5 paź 13:40
ola: pomocy proszę o wyjaśnienie powyższego zadania
5 paź 13:42
dero2005:
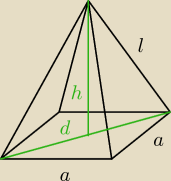
a =
√2
l =
√3
liczymy przekątną d
d = a
√2 = 2
liczymy wysokość z pitagorasa
h =
√l2 − (d2)2 = 1
5 paź 17:14
Kicia:*: 1.w ostrosłupie prawidłowym czworokątnym o krawedzi podstawy ma długość 4cm, a krawedz boczna
tworzy z płaszczyzną podstawy kąt 60 stopni. oblicz objętość ostrosłupa.
2.przekrój osiowy stożka jest trójkątem prostokątnym o polu 2. oblicz pole podstawy i objętość
stożka
5 kwi 08:36
Kicia:*: bardzo pilne

5 kwi 08:36
aniabb:
d=4√2 = l
h=2√6
V=1/3 42 * 2√6 = 32√6 / 3
5 kwi 08:41
aniabb: l=√2*2 = 2
2r=2√2 ⇒r=√2
Pp = πr2 = 2π
V=1/3 *2π * √2
5 kwi 08:43
Tedii: Przekątna ma długość √18cm. Ile jest równa objętość sześcianu
10 kwi 11:54
10 kwi 12:15
ja95: W ostrosłupie prawidłowym czworokątnym krawędź boczna o długości 16 cm tworzy z krawędzią
podstawy kąt 30stopni.
a) Oblicz gługość krawędzi podstawy.
b) długość wysokości ostrosłupa
c) długosc wysokości sciany bocznej
2 paź 19:41
dero2005:
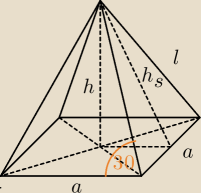
l = 16
a)
a = l
√3 = 16
√3
b)
d = a
√2 = 16
√6
h =
√l2 − (d2)2 =
√162 − (8√6)2 =
zadanie jest źle przepisane
2 paź 21:29
zacass: 2
11 kwi 23:54

 Długośc niebieska wynosi 4
Z sin60 wyliczamy wysokosc"
sin60=H/4
\tfrac{\sqrt{3}}{2} =H/4
H=2√3
V=1/3*64*2√3=128√3/3 cm3
Długośc niebieska wynosi 4
Z sin60 wyliczamy wysokosc"
sin60=H/4
\tfrac{\sqrt{3}}{2} =H/4
H=2√3
V=1/3*64*2√3=128√3/3 cm3
 a=8cm
α=60 stopni
y=H
a=8cm
α=60 stopni
y=H
 a= √2 , H >0
a= √2 , H >0
 a = √2
l = √3
liczymy przekątną d
d = a√2 = 2
liczymy wysokość z pitagorasa
h = √l2 − (d2)2 = 1
a = √2
l = √3
liczymy przekątną d
d = a√2 = 2
liczymy wysokość z pitagorasa
h = √l2 − (d2)2 = 1

 l = 16
a)
l = 16
a)