geometria analityczna Kacperix: Dany jest romb o wsporzednych A(0,−3) B(6,−5) C(4,1) D(−2,3), oblicz cosinus kąta rozwartego rombu. 1. Obliczylem wspolrzedne wektora BA[−6,2] i potem wektora BC[−2,6].

	−6*(−2)+6*2		3√10
2. Zatem cosx=		=		po wszelkich kosmetycznych
	√36+4+√36+4		5

zabiegach 3. aczkolwiek odpowiedz podaje ze cos tego kata to −0,6 Co robię źle

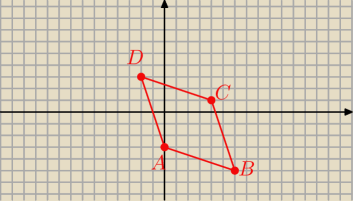
Janek191: Kąt ABC nie jest rozwarty.

Metis: Z resztą widać po znaku jaki otrzymałeś.

Kacperix: mi wychodzi coinus kąta DAB taki sam jak ABC tylko ze w minusie

Kacperix: policzylem wektory ab a ad i taki wynik , dlaczego

Mila: BA→ o BC^→=|BA|*|BC|*cosB A(0,−3) B(6,−5) C(4,1) D(−2,3), BA^→=[−6,2] BC^→=[−2,6] BA→ o BC^→=12+12=24 24=√6²+2²*√2²+6²*cosB 24=√40*√40*cosB 24=40*cosB

	24		3
cosB=		=		>0 ⇔∡B=∡D jest ostry
	40		5

∡A=180^o−∡B

	3
cosA=−		=−0,6
	5

Kacperix: czy mozesz wytłumaczyć mi swoją idee? dlaczego nie skorzystalas po prostu ze wzoru na cosinus kata miedzy dwoma niezerowymi wektorami nie bardzo wiem z czego korzystasz

Mila: Korzystałam z iloczynu skalarnego z którego masz wzór. Ty źle zapisałeś ten wzór, konkretnie mianownik.

	a o b
cos α=
	|a|*|b|

https://matematykaszkolna.pl/strona/1630.html

Mila: Mogłeś skorzystać z tw. cosinusów. Spróbuj tak zrobić.