Trójkąt o wierzchołkach a(6,0) b(o,y) c(0,0) jest prostokątny. oblicz y, jeżeli Pik: Trójkąt o wierzchołkach a(6,0) b(o,y) c(0,0) jest prostokątny. oblicz y, jeżeli promien okregu wpisanego w ten trojkat jest rowny 2. Prosiłbym o jakieś wskazówki, głównie chodzi mi o metodę. A metoda, która przychodzi mi na myśl jest czasochłonna i niektóre dane po prostu wziąłem, dzięki temu, że rozrysowałem odpowiednio.

Tadeusz:

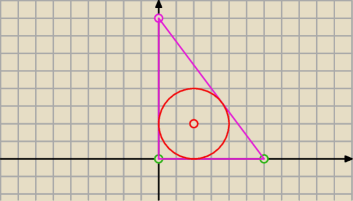
	6y
Twój trójkąt ma pole S=		=3y
	2

	2P
r=		i chyba wszystko jasne
	obwód

Pik: Nie za bardzo, nie znam tego wzoru i w tablicach też nie mogę go znaleźć. Może nie mam tych najnowszych. W takim wypadku prosiłbym o rozwiązanie, może uda się i bez tego wzoru na r. (w tym wzorze obwód tyczy się trójkąta, czy okręgu?).

Tadeusz: ... no nie żartuj https://matematykaszkolna.pl/strona/542.html

Tadeusz:

Tadeusz: albo tak jak powyżej

Tadeusz: oczywiście dwa rozwiązania y₁=8 y₂=−8

Pik: Okej, wzór rozumiem Kiedy podstawiam m.in. 3y do tego wzoru i r, to pozostaje kwestia dwóch boków, które kończą się w punkcie C. Jak obliczyć te długości, bo przychodzi mi na myśl, żeby np. poprowadzić prostą styczną do okręgu i mająca punkt np. (6;0) a następnie x=0 podstawić do tej prostej i wyjdzie y. Im więcej sposobów, podpowiedzi tym bardziej wdzięczny będę

Tadeusz: najłatwiej rozwiązując równanie z postu o 21:30

Pik: Kwestia dwóch boków, których długości nie wiem, jak zapisać...

Pik: Help :c

Tadeusz: ale wiesz. że trójkąt jest prostokątny ... i znasz twierdzenie Pitagorasa

Pik: Jasne, ale znam tylko jeden bok. Jak na razie ; d Ten jeden obliczyłem, że 6−0=0, a innych nie mogę ugryźć za nic

Pik: Czy drugi bok to ma np. długość y? i wtedy 6²+y²= ten trzeci bok² ?

Tadeusz: już chyba nie myślisz Drugi bok to y a trzeci to √36+y²

Tadeusz: dokładnie .... i w tedy w podanym wzorze masz jedną niewiadomą właśnie y

Pik: No właśnie wyżej wiadomość coś zaświeciło... Dobra to rozwiązuję. P=3y r=2P/a+b+c 2=(6y)/(6+y+√36+y²) √36+y²=2y−6/do ² 36+y²=4y²−24y+36 0=3y²−24y y²−8y=0 Δ=64 y1=(8−8)/2 − i to mi nie wychodzi y2=(8+8)/2=8 i to jest ok. Gdzie popełniłem błąd?

Tadeusz: oj chopie y²−8y=0 y(y−8)=0 y₁=0 sprzeczny w warunkach zadania y₂=8

Pik: No tak, nie może być zero. Jest druga odpowiedź, która pisałeś y= −8. czy wtedy po prostu rozważamy bok "drugi", że jest równy: −y ?

Tadeusz: on jest też równy 8 długość boku tyle, że punkt ma współrzędne (0, −8)

Pik: Yhym. Ale jeśli mamy współrzędną B(0,y) to raczej w tym zapisie y nie oznacza długości. Jako bok, owszem, ale już gdy mamy ja wrzucić do współrzędnej to pojawia się tylko jeden wariant B(0,8). Stąd moje zakłopotanie...

Tadeusz: długość boku zawartego dla BC dla B−(0, y) i C+(0, 0) to:√(0−0)²+(y−0)²=√y²=|y|

Pik: Chyba z żadnych obliczeń nie wyjdzie to drugie y tylko trzeba jakby na ten wariant samemu wpaść, że okrąg o tym promieniu itp. może być również w IV ćwiartce. Wielkie dzięki Tadeusz, czasem właśnie najprostsze rzeczy(tutaj np. że bok jest równy y) bywają najtrudniejsze

Pik: Super! Dziękuję!

Tadeusz: