Czworokąt wpisany w okrąg, dane jest pole trójkąta i długości dwóch boków
qwerty: Na czworokącie ABCD można opisać okrąg. Pole ostrokątnego trójkąta ACD jest rowne 12, |AD|=8,
|CD|=6. Oblicz miarę kąta CBA oraz promień okręgu.
Myślę, myślę i nie wiem od której strony ugryźć to zadanko

proszę o pomoc
24 lut 17:16
Tadeusz:
banalne

24 lut 17:27
Tadeusz:
ze wzoru na pole ΔACD policzysz sin ∡ADC
a potem twierdzenie o kątach czworokąta na którym można opisać okrąg
24 lut 17:30
qwerty:
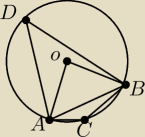
A no faktycznie, dziękuję bardzo !

więc sin =
12 tzn ∡ADB= 30 ⇒ ∡ACB= 150
⇒ ∡AOB = 60 ⇒trójkąt AOB jest równoboczny, próbowałam ze wzoru Herona ale wychodzi kosmos. Jak
inaczej wyliczyć promień?
24 lut 18:05
24 lut 18:08
qwerty:
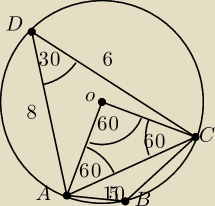
tak, ale... albo potrzebujemy długości boku AC albo kąta ∡DAC lub ∡ACD
(z czego to wyliczyć? )
24 lut 20:15
 proszę o pomoc
proszę o pomoc
 banalne
banalne 
 A no faktycznie, dziękuję bardzo !
A no faktycznie, dziękuję bardzo !  więc sin = 12 tzn ∡ADB= 30 ⇒ ∡ACB= 150
⇒ ∡AOB = 60 ⇒trójkąt AOB jest równoboczny, próbowałam ze wzoru Herona ale wychodzi kosmos. Jak
inaczej wyliczyć promień?
więc sin = 12 tzn ∡ADB= 30 ⇒ ∡ACB= 150
⇒ ∡AOB = 60 ⇒trójkąt AOB jest równoboczny, próbowałam ze wzoru Herona ale wychodzi kosmos. Jak
inaczej wyliczyć promień?
 tak, ale... albo potrzebujemy długości boku AC albo kąta ∡DAC lub ∡ACD
(z czego to wyliczyć? )
tak, ale... albo potrzebujemy długości boku AC albo kąta ∡DAC lub ∡ACD
(z czego to wyliczyć? )