Oblicz ekstrema i zbadaj monotoniczność funkcji ania: f(x) = x^2/3 (x² − 16)

Janek191: f(x) = x^2₃*( x² − 16) = x^8₃ − 16 x^2₃; x ≥ 0 więc

	8		2
f '(x) =		x53 − 16*		x−13 = 0 ⇔ x = 2
	3		3

	40		32
f '' (x) =		x23 +		x−43
	9		9

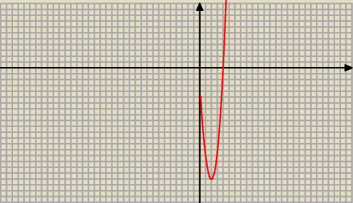
f ''(2) > 0 więc funkcja f ma w punkcie x = 2 minimum lokalne. Dla x < 2 jest f '(x) < 0 − f. maleje Dla x > 2 jest f '(x) > 0 − f. rośnie

5-latek: Janek191 spojrz tutaj https://matematykaszkolna.pl/forum/315856.html