Udowodnij. Michał: Zadanie dowodowe: x²+xy+y²≥3(x+y−1) Wszystko przeniosłem na jedną stronę, pomnożyłem * 2 stronami i chciałem zrobić (x−y)²+(x+..)²+(y+..)², ale zostawały wyrazy wolne..

Godzio: x² − 2x + 1 + y² − 2y + 1 + xy − x − y + 1 ≥ 0 ⇔ (x − 1)² + (y − 1)² + x(y − 1) − (y − 1) ≥ 0 ⇔ (x − 1)² + (y − 1)² + (y − 1)(x − 1) ≥ 0 / * 2 ⇔ (x − 1)² + 2(y − 1)(x − 1) + (y − 1)² + (x − 1)² + (y − 1)² ≥ 0 ⇔ [ (x − 1) + (y − 1) ]² + (x − 1)² + (y − 1)² ≥ 0 Co dowodzi początkowej nierówności.

Michał: Dziękuję. A jak zrobić to? Założenie: x+y=1 Teza: x³+y³≥1/4 4x³+4y³≥1 Potem pod 1 podstawić kwadrat (x+y) czy sześcian? O ile to jest dobra droga.

Godzio: x³ + y³ = (x + y)(x² − xy + y²) = x² − xy + y²

	1
x2 − x * y + y2 −		≥ 0 oraz y = x − 1
	4

i masz zwykłą funkcję kwadratową

Michał: Jak na to wpadłeś? Siedziałem kilka godzin nad tymi przykładem i nic nie wymyśliłem. Tak samo te przykłady: 1. Założenie: x²+y²+z²=1 Teza: (x−y)²+(y−z)²+(z−x)²≤3 2. Założenie: x,y,z>0 i xy+yz+zx>x+y+z Teza: x+y+z>3 3. Założenie: x+y+z=1 Teza: xy+yz+zx≤1/3 Z góry dziękuję za jakiś pomysł na to.

Michał: Podrzuci ktoś jakiś pomysł? To są trzy różne przykłady.

Jack: 1) (x−y)² = x² − 2xy + y² (y−z)² = y² − 2yz + z² (z−x)² = z² − 2xz + x² więc x² − 2xy + y² + y² − 2yz + z² + z² − 2xz + x² ≤ 3 2x² + 2y² + 2z² − 2xy − 2xz − 2yz − 3 ≤ 0 ze wzoru (x+y+z)² = x² + y² + z² + 2xy + 2xz + 2yz = 1 + 2xy + 2xz + 2yz −>>> czyli − 2xy − 2xz − 2yz = 1 − (x+y+z)² 2 − 2xz − 2yz − 2xy − 3 ≤ 0 −1 − 1 + (x+y+z)² ≤ 0 −2 + (x+y+z)² ≤ 0 o kurde... cos chyba nie tak daj chwile

Jack: ostatnie linijki skopalem, bo tam jest plus a nie minus... 2 − 2xz − 2yz −2xy −3≤0 −1 +(1− (x+y+z)²)≤0 −(x+y+z)²≤0 c.n.u

Jack: oczywiscie na poczatku komentarz przeksztalcajac nierownosc rownowaznie otrzymuje : ... i na koncu jakis tez by sie przydal : D

Eta:

	1
x+y=1 to x3+y3≥
	4

z nierówności między średnią potęgową i średnią arytmetyczną

	x3+y3		x+y
3√		≥		|3
	2		2

x3+y3		1
	≥		/*2
2		8

	1
x3+y3≥
	4

Jack: ahh te średnie...

Eta:

	1
3/ x+y+z=1 to xy+yz+xz≤
	3

Ponownie z nierówności między średnimi potęgową i arytmetyczną

	x2+y2+z2		x+y+z
√		≥		/2
	3		3

x2+y2+z2		1
	≥		/*3
3		9

	1
x2+y2+z2≥
	3

	1
(x+y+z)2−2(xy+xz+yz)≥
	3

	1
2(xy+xz+yz)≤1−		/:2
	3

	1
xy+xz+zy≤
	3

Eta:

Michał: @Eta: Nie ma innego wyjścia niż zależność między średnią potęgową a arytmetyczną?

Jack: 3/ po prostu bez zadnych srednich : (x+y+z)² = x² + y² + z² + 2xy + 2xz + 2yz skoro x+y+z = 1, to (x+y+z)² = 1 czyli 1 = x² + y² + z² + 2xy + 2xz + 2yz

1 − (x2 + y2 + z2)
	= xy + xz + yz
2

Przeksztalcajac nierownosc rownowaznie (ta z polecenia)

	1
xy + yz + xz −		≤ 0
	3

1 − (x2 + y2 + z2)		1
	−		≤ 0
2		3

3 − 3(x2+y2+z2)		2
	−		≤ 0 /// * 6
6		6

1 − 3(x²+y²+z²) ≤ 0 kurcze...myslalem ze 1 sie skroci... hmmm : (

Jack: albo inaczej 3) zrobmy sposobem −> podstawmy , wymnozmy wszystko w hit, a moze wyjdzie...

	1
xy + xz + yz −		≤ 0 /// (* 3)
	3

3xy + 3xz + 3yz − 1 ≤ 0 skoro x+y+z = 1, to wyciagamy np. x, czyli x = 1 − y − z 3y(1−y−z) + 3z(1−y−z) + 3yz − 1 ≤ 0 3y − 3y² − 3yz + 3z − 3zy − 3z² + 3yz − 1 ≤ 0 − 3y² − 3z² + 3y + 3z − 3zy − 1 ≤ 0 /// * (−1) 3y² + 3z² +3zy − 3y − 3z + 1 ≥ 0 (y+z)² + 2y² + 2z² + zy − 3y − 3z + 1 ≥ 0 (y+z)² + (y−1)² + (z−1)² + y² + z² − y − z + 1 + zy ≥ 0 // (* 2) 2(y+z)² + 2(y−1)² + 2(z−1)² + 2y² + 2z² − 2y − 2z + 2 + 2zy ≥ 0 2(y+z)² + 2(y−1)² + 2(z−1)² + (y−1)² + (z−1)² + y² + z² + 2zy ≥ 0 2(y+z)² + 2(y−1)² + 2(z−1)² + (y−1)² + (z−1)² + (y+z)² ≥ 0 czyli tak wlasciwie jak uporzadkujemy : 3(y+z)² + 3(y−1)² + 3(z−1)² ≥ 0 c.n.u heheh, wyszlo : D

Michał: A to jakim sposobem? x³<xy² /:x x²<y² x<y A w założeniu jest 0<x<y, więc jak to zapisać? 2. (xy)²+(yz)²+(zx)²−xyz(x+y+z)≥0 Założenie: xyz>0

Jack: 1) x³ < xy² x³ − xy² < 0 x(x²−y²) < 0 co jest prawdą, bo y > x, wiec nawias (x²−y²) będzie ujemny, a skoro zarowno x, jak i y sa dodatnie, to cale wyrazenie x(x²−y²) bedzie ujemne.

Jack: co Ty tyle udowadniasz...daj se spokoj : D

Michał: A jak z tym? 2. (xy)²+(yz)²+(zx)²−xyz(x+y+z)≥0 Założenie: xyz>0

Jack: (xy)² + (yz)² + (zx)² − xyz(x+y+z) ≥ 0 Przeszksztalcajac nierownosc rownowaznie, otrzymujemy : (najpierw wszystko wymnazamy) x²y² + y²z² + z²x² − x²yz − y²xz − z²xy ≥ 0 // * 2 x²y²+x²y² + y²z²+y²z²+z²x²+z²x²− 2x²yz−2y²xz−2z²xy≥ 0 x²(y² + z² − 2yz) + y²(x² + z² − 2xz) + z²(y² + x² − 2xy) ≥ 0 x²(y−z)² + y²(x−z)² + z²(y−x)² ≥ 0 c.n.u.

Michał: "Zadanie 2: Założenie: x+y=1 Teza: x3+y3≥1/4 Godzio: x3 + y3 = (x + y)(x² − xy + y²) = x² − xy + y² x² − x * y + y² − 0.25 ≥ 0 oraz y = x − 1 i masz zwykłą funkcję kwadratową " Chyba y=1−x z założenia, a więc podstawię do funkcji kwadratowej: x²−x*(1−x)+(1−x)²−0.25≥0 x²−x+x²+1−2x+x²−0.25≥0 3x²−3x+0.75≥0 Δ=(−3)²−4*3*0.75=9−9=0 x=3/(2*3)=1/2 I co z tym dowodem dalej?

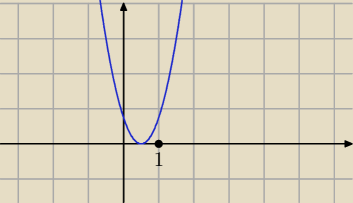
Jack: wychodzi CI tylko jedno miejsce zerowe : x = U{1}[2} i to jest prawda bo to jest wieksze lub rowne zero.

	1
W zadnym punkcie nie przecina osi, tylko w punkcie (		,0) sie styka, czyli w tym punkcie
	2

jest =0, a wszedzie indziej >0, wiec ogolnie ≥0

Michał: Dobra, a jak to zapisać? 0.5≥0 c.n.u jest chyba zbyt ubogie i przydałby się dłuższy wniosek.

Jack: nie jestem zbyt dobry w pisaniu komentarzy... ale powinno byc cos w stylu 3x² − 3x + U{3}[4} ≥ 0

	1
3(x −		)2 ≥ 0
	2

x ∊ R, co nalezalo udowodnic

Michał: A więc nawet nie trzeba było liczyć delty i miejsca zerowego... Nie rozumiem, jeszcze jak @Godzio zrobił taką zamianę: (x − 1)2 + (y − 1)2 + x(y − 1) − (y − 1) ≥ 0 ⇔ (x − 1)2 + (y − 1)2 + (y − 1)(x − 1) ≥ 0 x(y − 1) − (y − 1)=(y − 1)(x − 1)

Jack: wyciagasz (y−1) przed wszystko tak samo jak bys mial x(x+1) −1(x+1) jak wyciagniesz x+1 to masz wlasciwie x(x+1) −1(x+1) = (x+1)i Ci zostaje(x − 1)

Michał: Teza: a+b=1 ⇒ (a+b)²=1 Założenie: a⁴+b⁴≥1/8 (a²−b²)²−2(ab)²≥1/8 No i po przekształceniach wyszło mi: 7(a−b)²−16(ab)²≥0 Gdyby tam był "+" to dowód byłby poprawny.. Da radę to inaczej przekształcić niż dzięki zależność między średnią potęgową a arytmetyczną?

Michał: Nikt nie wie?

Michał: "Jack: 3) zrobmy sposobem −> podstawmy , wymnozmy wszystko w hit, a moze wyjdzie... 3xy + 3xz + 3yz − 1 ≤ 0 skoro x+y+z = 1, to wyciagamy np. x, czyli x = 1 − y − z 3y(1−y−z) + 3z(1−y−z) + 3yz − 1 ≤ 0 3y − 3y² − 3yz + 3z − 3zy − 3z² + 3yz − 1 ≤ 0 − 3y² − 3z² + 3y + 3z − 3zy − 1 ≤ 0 /// * (−1) 3y² + 3z2 +3zy − 3y − 3z + 1 ≥ 0 (y+z)² + 2y² + 2z² + zy − 3y − 3z +1 ≥ 0 (y+z)² + (y−1)² + (z−1)² + y² + z² − y − z + 1 + zy ≥ 0 // (* 2) 2(y+z)² + 2(y−1)² + 2(z−1)² + 2y² + 2z² − 2y − 2z + 2 + 2zy ≥ 0 2(y+z)² + 2(y−1)² + 2(z−1)² + (y−1)² + (z−1)² + y2 + z2 + 2zy ≥ 0 2(y+z)² + 2(y−1)² + 2(z−1)² + (y−1)² + (z−1)² + (y+z)² ≥ 0 czyli tak wlasciwie jak uporzadkujemy : 3(y+z)² + 3(y−1)² + 3(z−1)² ≥ 0 c.n.u heheh, wyszlo : D" Zaznaczone na czerwono. We wzorach użyłeś 1, której nie zabrałeś i w rezultacie liczba została zwiększona.

Kacper: biorę

Michał: Co bierzesz? Potrzebuję pomocy :c

Kacper: Kilkakrotnie było to zadanie. Pokazałem 2 lub 3 metody jego rozwiązania. Szukaj.

Michał: Szukałem i nie ma, gdybym to znalazł to bym nie pisał o pomoc.

Kacper: XIX wiek, a zero zaradności wśród młodzieży, co tak się chwali, ze wszystko potrafi z komputerem zrobić. 310617

Michał: Oj chyba ktoś nie potrafi czytać.. Mam problem z tym przykładem: 3. Założenie: x+y+z=1 Teza: xy+yz+zx≤1/3 Jack go rozwiązał, ale błędnie. Na czerwono zaznaczyłem te nieścisłości..

Ewa: Oblicz −(x²−xy−z)−(−x²+2xy+2z)=