Wykaż
Dżin: Wykaż, że jeśli a i b są liczbami rzeczywistymi dodatnimi oraz a+b=1, to spełniona jest
28 gru 17:14
Saizou :
z nierówność o średnich mamy że
| | a4+b4 | | a+b | | 1 | |
( |
| )1/4≥ |
| = |
| /4 |
| | 2 | | 2 | | 2 | |
28 gru 17:20
Dżin: Dzięki
Saizou, ale nierówności o średnich w liceum nie miałem i nie będę mieć, więc
poproszę o prostsze rozwiązanie

28 gru 17:30
Kacper:
a=1−b
a
4+b
4=2b
4−4b
3+6b
2−4b+1
Niech f(b)=2b
4−4b
3+6b
2−4b+1
Szukamy ekstremów globalnych funkcji f.
f'(b)=8 b
3−12 b
2+12 b−4
Analizując pierwszą i drugą pochodną dochodzimy do wniosku, że funkcja f osiąga minimum dla
| | 1 | | 1 | | 1 | |
b= |
| równe |
| , zatem a4+b4≥ |
| . |
| | 2 | | 8 | | 8 | |
Proszę inne rozwiązanie, ale czy łatwiejsze?

28 gru 17:42
Dżin: haha, pochodna to ostatnia rzecz którą bym stosował jakbym miał takie zadanie na maturze

ale
dział w którym jest to zadanie to "stosowanie wzorów skróconego mnożenia"


28 gru 17:54
Jack: no i prawidlowo
ja bym probowal raczej
(a2 +b2)2 − 2a2b2
wiedzac ze
a+b = 1
(a+b)2 = 1 = a2 + 2ab + b2
28 gru 17:58
Dżin: Liczę, liczę i nie mogę się doliczyć, jednak pozostanę przy pochodnych...

28 gru 18:42
Jack: co tak szybko sie poddales ; D
to ze ja tez tego nie umiem... to nic xd
28 gru 18:43
Dżin: nie poddałem się, porobię mniej "ambitne" zadania i spróbuje podejść jeszcze raz do tego
zadania, jeszcze wrócę z rozwiązaniem

28 gru 18:50
Kacper:
Jak nie wymyślicie w ciągu godziny, to podam jeszcze 2 inne rozwiązania

28 gru 18:50
Jack: pochodna czy srednia jakas tam to dla mnie takie srednie rozwiazania... dwumian newtona tutaj
tez wg mnie srednio pasi
28 gru 19:03
Dżin: (a
2−b
2)
2≥0
a
4+b
4≥2a
2b
2
| | 1 | | 1 | |
(a−b)2≥0 → (a+b)2≥4ab → |
| ≥ab → |
| ≥2a2b2 |
| | 4 | | 8 | |

28 gru 19:07
Jack: nwm czy to cos udowadnia? ;x
28 gru 19:11
Kacper:
Z faktu, że a>b i c>b nie wynika, że a>c

28 gru 19:12
Dżin: Dobra
Kacper, wrzucaj te rozwiązania

28 gru 19:40
Jack: nie ma xd
28 gru 20:56
zeesp: a+b=1
a
4+b
4=(a
2+b
2)
2−2(ab)
2
=((a+b)
2−2ab)
2−2(ab)
2
=(1−2ab)
2−2(ab)
2
=1−4ab+4(ab)
2−2(ab)
2
=1−4ab+2(ab)
2
=2(ab)
2−4ab+1
Wniosek a
4+b
4 jest najmniejsze gdy (ab−1)
2 jest najmniejsze
1. Jeżeli a=0 lub b=0 (oraz jak wiemy a+b=1) to b=1 lub a=1, w każdym razie a
4+b
4=1 i
nierównosc jest ok
2. Jeżeli a>0 i b>0 to a*b<1 (żeby a+b=1) więc ab−1<0
Więc (ab−1)
2 najmniejsze jeżeli ab−1 największe
| | 1 | |
a+b=1 więc b=1−a wiec ab−1=a(1−a)−1=−a2+a−1 ma wartość największą dla a= |
| |
| | 2 | |
| | 1 | | 3 | | 9 | |
w konsekwencji a*b= |
| oraz (ab−1)2=( |
| )2= |
| |
| | 4 | | 4 | | 16 | |
| | 1 | | 9 | | 1 | | 9 | | 8 | | 1 | | 1 | |
2[(ab−1)2− |
| ]=2( |
| − |
| )=2( |
| − |
| )=2*( |
| )= |
| |
| | 2 | | 16 | | 2 | | 16 | | 16 | | 16 | | 8 | |
I jak pokazaliśmy wyżej gorzej już nie będzie

28 gru 20:58
zeesp: Wygląda strasznie...i dośc długo...ale starałem się jak najabrdziej elementarnie
28 gru 20:58
Jack: ja doszedlem do tego msca : 2(ab)2−4ab+1
28 gru 21:02
Jack: aczkolwiek srednie uzasadnienie : D
28 gru 21:06
zeesp: Też bym to zrobił inaczej, ale wychodząc z zalożenia, że ktoś nie ma żadnych narzędzi to tu nic
sie nie dzieje

28 gru 21:09
Dżin: zeesp dzięki, ja bym na to nie wpadł
 Jack
Jack według Ciebie wszystko jest średnie

28 gru 21:11
Jack: bo ja oczekuje wiesz, prostego rozwiazania ze pokazesz typu
(a−b)
2 ≥ 0
i to dla mnie jest dowod

28 gru 21:12
Dżin: Ale to takie 2/10

Ciekawe jak zrobi
Kacper..

28 gru 21:14
Saizou : Tak jak moja odpowiedź

28 gru 21:35
Jack: to o srednich to juz wgl.. : D
28 gru 21:41
Benny: @Kacper Ty miales nierownosci miedzy srednimi w liceum?
28 gru 21:44
Jack: niektorzy juz calki w liceum liczyli...
28 gru 21:49
Dżin: Jack Rachunek różniczkowy jest w programie

28 gru 22:09
Jack: rachunek rozniczkowy to ja mialem...i skonczylo sie na pochodnym
28 gru 22:11
Jack: pochodnych*
a calek juz sie nie rusza
28 gru 22:12
bezendu:
Po co Ci całki w liceum ? Będziesz liczyć pole wykresu, pomiędzy funkcjami, liczyć objętość
brył w układzie 3 współrzędnych ?
Nawet nie znasz definicji całki więc nie gorączkuj się tak, nauczysz się w swoim czasie.
28 gru 22:15
Jack: definicji nie znam, ale podstawowe wzory juz tak : D
28 gru 22:16
bezendu:
No i co z tego, że znasz wzory jak nie wiesz co liczysz...
Bez komentarza... Czyli tylko wykuć wzory, a nie wiedzieć co się liczy

28 gru 22:17
Jack: jak musze policzyc pole np. w paraboli, to licze calke, i tyle
28 gru 22:17
bezendu:
Pole w paraboli, to ja nawet tego nie potrafię

Co innego policzyć pole zawarte pomiędzy parabolą a jakąś wykresem jakieś funkcji.
I właśnie pokazałeś, że nie wiesz co to jest całka i do czego służy

K.O
28 gru 22:20
Dżin: bezendu rachunek różniczkowy na poziomie licealnym to przeważnie(bądź tylko) zadania
optymalizacyjne

28 gru 22:21
Jack:
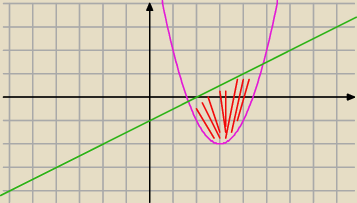
mam na mysli takie cos (pole zaznaczone czerwonymi kreskami)...
zawsze mam tak, ze moje slowa nie wyrazaja tego co mysle ; )
28 gru 22:22
bezendu:
Więc własnie nie wiem po co mu teraz całki skoro w liceum jest tyle fajnego materiału do nauki.
A tym bardziej wątpię żeby w lo liczyło się pole ograniczone krzywymi

28 gru 22:23
Jack: "fajny materiał"
hmm, jestem bardzo ciekaw, co tam jest fajnego

28 gru 22:23
Dżin: Matematyka sama w sobie jest fajna

28 gru 22:24
Jack: najtrudniejsze dzialania to dodawanie i odejmowanie
8+5 zawsze sprawdzam na kalkulatorze...
28 gru 22:26
28 gru 22:27
Jack: planimetria , trygonometria i ogolnie bryly to temat ktorego najbardziej nie lubie... a co tu
robie ? na tym forum 99% zadan ktore dostaje to jakies trojkaty do obliczenia...otwieram ten
link i co? kolejne trojkaty... ehhh
28 gru 22:28
bezendu:
Kolejne trójkąty, ale nie udowodnisz żadnego zadania w tym pliku, chyba, że znajdziesz gotowca
na necie

28 gru 22:29
Jack: twierdzenie ptolemeusza?!
28 gru 22:29
Jack: challenge accepted...

chociaz jedno udowodnie !
28 gru 22:29
Dżin: Chłopaki.. nie róbcie mi tutaj offtopa bo
Kacper się wystraszy, i co? nie będzie jego
rozwiązań

28 gru 22:33
Jack: lujowe to zadania
w sensie nietypowe : D
28 gru 22:35
zombi: Akurat 1. z Pompe jest banalne XD tak jak nienawidzę plani to pierwsze bym zrobił

28 gru 22:42
Eta:
a>0, b>0 i a+b=1 to ab∊(0,1)
a+b=1 /
2 ⇔ a
2+b
2=1−2ab
i a
4+b
4 = (a
2+b
2)
2−2a
2b
2 = (1−2ab)
2−2a
2b
2= 2a
2b
2−4ab+1
| | 1 | | 7 | |
to a4+b4≥ |
| ⇔ 2a2b2−4ab+ |
| ≥0 Δ= 9 |
| | 8 | | 8 | |
| | 4+3 | | 4−3 | | 1 | | 1 | |
ab= |
| >1 −−− odrzucamy lub ab= |
| = |
| ⇔ 2a2b2= |
| |
| | 4 | | 4 | | 4 | | 8 | |
ze znanej nierówności a
4+b
4≥2a
2b
2
c.n.u

28 gru 22:46
Dżin: Dzięki
Eta!

28 gru 22:52
Jack:
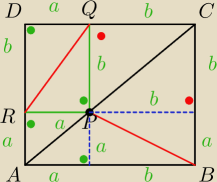
|PB| =
√a2+b2
|RQ| =
√a2+b2
28 gru 22:55
Jack: i co, pierwsze zrobilem !
28 gru 22:55
Jack: wszystkie katy proste powiedzialy co mamy robic ; D
i ze to jest kwadrat...
28 gru 22:56
Jack: aczkolwiek nadal nie wiem co to jest rzut prostokatny...i czy to ma znaczenie tutaj : D
28 gru 22:57
Benny: @
bezendu widzisz, ja jeszcze całek nie miałem, a w liceum już mają

28 gru 23:07
Jack: nie mamy wlasnie, Benny...
28 gru 23:10
Jack: tylko gdybym trzymal poziom tego co mamy, to bym nie rozwiazal najprostszych nierownosci... : D
sam musze sie "douczac"
28 gru 23:11
Benny: Ja na Twoim miejscu też bym się douczał, ale bez sensu całek czy równań różniczkowych. Porób
sobie jakieś OMG lub jeśli jesteś zdolny to OM

28 gru 23:24
Jack: @ Dżin
ewentualnie
zaczne juz od momentu
2a
2b
2 − 4ab + 1 = (
√2ab −
√2)
2 −
√2 + 1
obustronny pierwiastek
√2ab −
√2 ≥ (
√−78 + √2) <−−ten warunek odpadnie potem...
lub
−
√2ab +
√2≤ (
√−78 + √2) / *(−1)
√2ab −
√2 ≥ (
√−78 + √2)
b = 1− a
√2a(1−a) −
√2 ≥(
√−78 + √2)
liczymy wierzcholek, bo tam jest minimum
.
.
.
za duzo pisania...
po porownaniu, na koncu wyjdzie
√2 < 4
c.n.u....
28 gru 23:28
zombi: Rób zadania konkursowe, pomagają rozwijać myślenie. Prawda jest taka, że zadania maturalne to w
95% schematy. System edukacji zapomina o tym, co w matematyce najważniejsze, myśleniu!
28 gru 23:28
Jack: oczywiscie tyle rownan bez sensu wykonywac xd
@Benny
Co to OMG / OM ?
28 gru 23:29
Jack: no wlasnie ja wgl nie mysle ; D
28 gru 23:29
zombi: Olimpiada matematyczna gimnazjalistów (którą zlikwidowali) oraz Olimpiada matematyczna dla
uczniów szkół średnich.
28 gru 23:30
28 gru 23:31
Jack: zlikwidowali? ; o
28 gru 23:31
Jack: sugerujesz, ze jestem az tak slaby, ze tylko poziom gimnazjum bd umial zrobic? w klasie
maturalnej...
28 gru 23:31
zombi: Była z tym sprawa związana, że MEN zlikwidował OMG, z niewiadomych albo wiadomych przyczyn. Ale
najwidoczniej wrócili do niej.
28 gru 23:32
zombi: Uwierz mi, że jeśli robiłeś jedynie zadania maturalne to nie tkniesz 80% zadań z gimnazjalnej

28 gru 23:32
Benny: Nic nie sugeruje. Nie wiem jaki jest Twój poziom.
28 gru 23:33
Jack: to wam powiem − > tak niski ze jak sie poloze na podlodze to moj poziom przebija podloge

28 gru 23:34
Jack: nie ma ktos zadan z funkcja wykladnicza/logarytmami
do sprawdzianu bym sie pouczyl

28 gru 23:37
Dżin: Znaleźć wszystkie rzeczywiste wartości a, dla których pierwiastki równania:
log
2(x+3)−2log
4x=a
należą do przedziału (3;4)
Działaj!

28 gru 23:44
Jack: | | log4 (x+3) | |
log2 (x+3) = |
| = 2 log4 (x+3) = log4 (x+3)2 |
| | log4 2 | |
log
4 (x+3)
2 − log
4 x
2 = a
28 gru 23:55
Benny: | | 1 | |
Zapamiętaj, że logabc= |
| logac |
| | b | |
28 gru 23:57
28 gru 23:59
Jack: @ Benny, co to za wlasnosc ? ; o
28 gru 23:59
Jack: dalej za bardzo nwm jak to zrobic : D
29 gru 00:01
Dżin: Uzupełnię wypowiedź
Bennego:
29 gru 00:03
Jack: ciekawe, a przyda mi sie tu ?

29 gru 00:04
Eta:

29 gru 00:05
Dżin: Tego to ja nie wiem

29 gru 00:06
Benny: Łatwo ją wyprowadzić.
| | logac | | 1 | |
logabc= |
| = |
| logac |
| | logaab | | b | |
29 gru 00:06
Jack: wiecej jak to ze
nie wymysle...nwm jak uwzglednic ten przedzial (3;4)
29 gru 00:07
Eta:
@
Benny widzę ,że nauka nie poszła na marne

29 gru 00:08
Benny: Jasne, że nie, tylko to ni jak mi się teraz przyda do egzaminu z logiki

29 gru 00:10
Eta:
Dasz radę i z logiką

29 gru 00:11
Jack: a mi to nikt nie pomoze

: D
29 gru 00:11
Godzio: Już jesteś na mecie,
| | 3 | |
2a = 1 + |
| ⇒ x = ... ∊ (3,4) |
| | x | |
29 gru 00:12
Mila:
Benny, czytaj teorię, wykłady − wtedy zrozumiesz. Analizuj przykłady z ćwiczeń.
29 gru 00:12
Jack: ... (tak wiem , jestem debilem)
29 gru 00:14
Dżin: Jack mam jeszcze jedno zadanie dla Ciebie, możesz zrobić po śniadaniu

Rozwiąż równanie:
| | 1 | | 1 | | 1 | | n | |
log2x+(log4x+ |
| log8x+ |
| log16x+...+ |
| log2n+1x)=2n− |
| |
| | 2 | | 3 | | n | | n+1 | |
x∊R n∊N
+
29 gru 00:15
Benny: Z tymi wykładami to nie byłym taki pewien. Większość z tego co mam napisane to nie wiadomo o
chodzi, nie tylko w moim przypadku. Przykłady z ćwiczeń to nawet nie ma o czym mówić, jedyna
nadzieja pozostaje w książkach

29 gru 00:16
Jack: | 3 | | 3 | |
| > 3 ⋀ |
| < 4 |
| 2a −1 | | 2a −1 | |
29 gru 00:17
Jack: z pierwszego
a ∊ (0;1)
z drugiego
chyba nie dam rady
| | 7 | |
mam ze a = 0 lub 2a = |
| ... |
| | 4 | |
paraboli z tego nie narysuje : D
29 gru 00:23
Jack: Any ideas?
29 gru 00:30
Godzio:
| 3 | |
| < 4 / * (2a − 1)2 i niech 2a − 1 = t > − 1 |
| 2a − 1 | |
3t < 4t
2
4t
2 − 3t > 0
t(4t − 3) > 0
2
a − 1 < 0 ⇒ 2
a < 1 ⇒ a < 0
| | 3 | | 7 | | 7 | |
2a − 1 > |
| ⇒ 2a > |
| ⇒ a > log2 |
| |
| | 4 | | 4 | | 4 | |
29 gru 00:30
Jack: Dlaczego
1) t > − 1
29 gru 00:34
Jack: Tak wgl to dzieki za pomoc
29 gru 00:36
Godzio:
2
a > 0 to 2
a − 1 > −1
29 gru 00:37
Jack: Hmm nwm jakndossedles do tego zapisu no ale niecj bedzie...
Co ciekawe a nalezy do zbioru pustego...
29 gru 00:40
Godzio:
Pytaj, po to tu jestem, żeby wytłumaczyć

W między czasie odrzuciliśmy a = 0, a to jest z pewnością rozwiązaniem

29 gru 00:43
Godzio:
A rozwiązanie to:
29 gru 00:46
Jack: Nie rozumiem jak z
Czyli przedostatnia i ostatnia linijka postj 00:30
29 gru 00:46
Godzio:
| | 7 | | 7 | |
Aaa, moje przeoczenie, oczywiście powinno być log2 |
| , a nie |
| |
| | 4 | | 4 | |
29 gru 00:47
Jack: I dlaczego 0 pasuje skoro zbiór obustronnie otwarty
29 gru 00:48
Jack: Aa...no dobra to teraz wszystko jasne
29 gru 00:49
Jack: Oprpcz tego zera

29 gru 00:49
Jack: Ja ide spac... Dziekuje za pomoc i dobranoc

29 gru 00:51
Godzio: Dzieląc przez 2
a − 1 wykluczasz a = 0, więc dla niego osobno trzeba sprawdzić co się dzieje.
| 3 | |
| = 0, a to nie ma rozwiązań (wcześniej się coś pomyliłem, późna pora  ) |
| x | |
29 gru 00:51
Godzio: Dobranoc

29 gru 00:53
Metis: | | 1 | | 1 | | 1 | | n | |
log2x+(log4x+ |
| log8x+ |
| log16x+...+ |
| log2n+1x)=2n− |
| |
| | 2 | | 3 | | n | | n+1 | |
| | 1 | | 1 | | 1 | |
log4x+ |
| log8x+ |
| log16x+...+ |
| log2n+1x |
| | 2 | | 3 | | n | |
| log2x | | 1 | | log2x | | 1 | | log2x | |
| + |
| * |
| + |
| * |
| +...= |
| log24 | | 2 | | log28 | | 3 | | log216 | |
| log2x | | log2x | | log2x | | log2x | |
| + |
| + |
| +...+ |
| |
| 2 | | 6 | | 12 | | n2+n | |
Jutro reszta

29 gru 01:35
Kacper:
Ale śmietnik

(Jadę na zakupy i rozwiązania podam jak wrócę)
Benny − nie miałem nierówności Cauchy'ego w LO, ale na studiach pisałem magisterkę o tym

Poza tym zadanie z logarytmem nie pójdzie bez znajomości pewnego twierdzenia.
Znam książkę, z której to zadanie wzięto. Zapewne autor sam nie umie go rozwiązać, ale na
szczęście tam jest pełne rozwiązanie

29 gru 08:58
Benny: Kurcze prawie mi wyszło

Dostałem 2
n(2n+1)/(n+1)=x
(2n+1)/(n+1) chyba, że sobie spierwiastkuje i dostanę x=2
n lub
jest błąd i x=2

29 gru 09:42
29 gru 12:01
Lorak: wolfram może nie zrozumieć ' + ... + '

29 gru 12:20
Jack: a tak na serio to banał takie zadanie
juz poczatku nie bd przepisywac...jestem zbyt leniwy : D
wiec mamy
| | 1 | | 1 | | 1 | | n | |
log2 x(1 + |
| + |
| + ... + |
| ) = 2n − |
| |
| | 2 | | 6 | | n(n+1) | | n+1 | |
| | 1 | | n | |
log2x (1 − |
| ) = 2n − |
| |
| | n+1 | | n+1 | |
| | 1 | | n | |
log2 x − log2x * |
| = 2n − |
| / * (n+1) |
| | n+1 | | n+1 | |
(n+1) log
2x − log
2 x = 2n(n+1) − n
log
2x (n+1 − 1) = 2n
2 + n
log
2 x*n = 2n
2 + n
.
.
.
hmm, tu chyba utknalem : D
29 gru 12:42
Benny: Źle od początku
undefined
29 gru 12:47
Jack: co jest niby zle ? ; d
29 gru 12:48
Benny: Jak wyciągnąłeś sobie log2x skoro wszędzie jest inna podstawa?
29 gru 12:51
Jack: oj benny, wszedzie jest ta sama....
29 gru 12:51
Benny: No chyba, że w pamięci sobie wszędzie zmieniłeś, ale i tak nadal źle.
29 gru 12:52
Jack: No jak majster no...paczaj
| | 1 | | 1 | | 1 | | n | |
log2x+(log4 x + |
| log8x+ |
| log16x+... + |
| log2n+1x)=2n − |
| |
| | 2 | | 3 | | n | | n+1 | |
| | 1 | | 1 | | 1 | | 1 | | n | |
log2x+ |
| log2 x+ |
| log2 x+ |
| log2x +...+ |
| log2n+1x=2n − |
| |
| | 2 | | 6 | | 12 | | n | | n+1 | |
log
2x( ...
29 gru 13:00
Jack: Wszystko sie zgadza...nwm w czym masz problem : D
29 gru 13:01
Benny: | | 1 | |
I mówisz, że suma 1+ |
| +... jest równa 1−coś? |
| | 2 | |
29 gru 13:02
Dawid: Kto szuka problemu ten go znajdzie

29 gru 13:02
Jack: oj Benny, kto Cie matmy uczył

to jest typowy ciąg nietypowy
ahahah, zapomnialem dodac jeden na koncu , faktycznie tam lekko skopalem
a co do tego ciagu
| 1 | | 1 | | 1 | | 1 | |
| + |
| + |
| + |
| + ... = |
| 2 | | 6 | | 12 | | 20 | |
| | 1 | | 1 | | 1 | | 1 | |
= |
| + |
| + |
| + |
| + ... = |
| | 1*2 | | 2*3 | | 3*4 | | 4*5 | |
| | 1 | | 1 | | 1 | | 1 | | 1 | | 1 | | 1 | |
= (1− |
| ) + ( |
| − |
| ) + ( |
| − |
| ) + ( |
| − |
| ) + ... |
| | 2 | | 2 | | 3 | | 3 | | 4 | | 4 | | 5 | |
29 gru 13:09
Benny: Specjalnie log
2x jest przed nawiasem, aby coś zauważyć

29 gru 13:09
Benny: @Jack coś sugerujesz?
29 gru 13:11
Jack: sugeruje ze sugerujesz ze sie myle, kiedy mam racje

29 gru 13:11
Metis: Mój post jest 1:35 jest

? Pisałem to w nocy

29 gru 13:12
Jack: 
29 gru 13:18
Metis: Benny ,
Kacper potwierdźcie

29 gru 13:19
Jack: co do tamtego mojego bledu
tak powinno byc...
| | 1 | | n | |
log2x + log2x (1− |
| ) = 2n− |
| |
| | n+1 | | n+1 | |
29 gru 13:19
Qulka: zgadzam się z
Jackiem

29 gru 13:23
Metis: 
29 gru 13:25
Qulka: aaa i obaj macie to samo

jakby nie było widać ..bo się chyba pogubiłam o co kto pytał

29 gru 13:30
Jack: no tak, tylko ja rozwinalem wypowiedz Metis
29 gru 13:31
Qulka: aa bo widziałam ten niżej i myślałam że liczyłeś oddzielnie

tak to jest jak post ma kilka
wątków

29 gru 13:35
Jack: to teraz niech ktos moj post rozwinie
| | 1 | | n | |
log2x(2 − |
| ) = 2n − |
| |
| | n+1 | | n+1 | |
29 gru 13:39
Benny: No zwykła równość logarytmiczna.
29 gru 13:42
Qulka: x=2n
29 gru 13:42
Metis: | | 1 | |
Skąd Ci się wzieło to 2− |
| |
| | n+1 | |
29 gru 13:42
Dżin: | | 1 | | 1 | |
log2x+log2x(1− |
| )=log2x[1+(1− |
| )] |
| | n+1 | | n+1 | |
29 gru 13:46
Jack: @Metis − log2x przed nawias
29 gru 13:47
Jack: @Qulka
Moglabys rozpisac : D
29 gru 13:48
Dżin: | | 2n+1 | | n(2n+1) | |
log2x* |
| = |
| |
| | n+1 | | n+1 | |
log
2x=n
x=2
n
29 gru 13:52
Jack: moge tak po prostu skrocic? ; o
29 gru 13:56
Jack: a, no tak, to mnozenie...to fajno ; D
x = 2n
wiec jednak to zadanko bylo do ogarniecia
29 gru 13:57
Dżin: n≠−1

29 gru 13:57
Jack: w poleceniu bylo ze "n" ∊ N
+ 
29 gru 14:00
Dżin: nie znasz się na żartach...


29 gru 14:04
Jack: Niestety nadal nie rozumiem co miał na myśli [Benny]...dwa razy mowil ze mam zle
29 gru 14:08
Kacper:
Ok to czas na zadanko:
Rozwiązanie (nie moje − zapożyczone)
Lemat:
Prawdziwa jest nierówność: (a
2+b
2)(c
2+d
2)≥(ac+bd)
2 (*)
(dowód zostawiam wam, bo jest prosty)
| | 1 | |
Aby dowieść nierówności x4+y4≥ |
| wystarczy pokazać, że: |
| | 8 | |
| | (x+y)4 | |
x4+y4≥ |
| ⇔ 8(x4+y4)≥(x+y)4 |
| | 8 | |
Korzystamy z lematu z danymi a=1, b=1, c=x, d=y
8(x
4+y
4)=4(1+1)(x
4+y
4)≥(*)≥4(x
2+y
2)
2=(1+1)(x
2+y
2)(1+1)(x
2+y
2)≥(*)
≥(x+y)
2(x+y
2)=(x+y)
4
c.k.d
29 gru 14:16
Dżin: Dzięki
Kacper!

29 gru 14:32
Benny: @Jack cały czas chodziło mi o tą 1, nie powiesz chyba, że miałeś dobry wynik.
29 gru 14:34
Kacper:
Jeszcze mam 2 rozwiązania, ale idę po drzewo teraz.
29 gru 14:35
Kacper:
Dżin jesteś on czy ona?
29 gru 14:35
Dżin: Dżin kobietą być nie może.

29 gru 14:38
Kacper:
Nigdy nie spotkałem się z faktem, że dżin musi być mężczyzną

29 gru 14:41
Jack: @Benny
no dobra... niech Ci bedzie : D
29 gru 15:08
Dżin: Kacper gdzie studiujesz?
29 gru 15:21
Kacper:
Dzin ja trochę starszy jestem i uczę w szkole.
29 gru 15:41
Dżin: Aha.
29 gru 15:48
Jack: Aha
. <−− kropka nienawiści

29 gru 16:47
Kacper:
Nienawiści? Dlaczego?

29 gru 18:40
Dżin: Heh, właśnie też nie wiem

29 gru 18:49
PW: Mniej skomplikowana wersja dowodu, nie wymagająca znajomości lematu przytoczonego przez
Kacpra:
Z faktu, że dla dowolnych u, v
(u − v)
2 ≥ 0
wynika
u
2 + v
2 ≥ 2uv
2u
2 + 2v
2 ≥ u
2 + v
2 + 2uv
(1) 2(u
2 + v
2) ≥ (u + v)
2.
Po podstawieniu u = x
2 i v = y
2 dostajemy
| | (x + y)2 | |
(2) 2(x4 + y4) ≥ (x2 + y2)2 ≥ ( |
| )2, |
| | 2 | |
przy czym ostatnia nierówność jest skutkiem ponownego zastosowania (1) ze zmienionymi
symbolami. Z (2) wynika
co oznacza że dla x + y ≥ 1 prawdziwa jest nierówność
Jak widać nierówność nie wymaga założenia x, y > 0 ani x + y = 1, wystarcza założenie
x + y ≥ 1.
29 gru 22:39
Kacper:
PW pięknie

rzeczywiście uproszczona wersja

30 gru 09:07
Dżin: Dzięki
PW 

30 gru 13:53


 ale
dział w którym jest to zadanie to "stosowanie wzorów skróconego mnożenia"
ale
dział w którym jest to zadanie to "stosowanie wzorów skróconego mnożenia" 









 Jack według Ciebie wszystko jest średnie
Jack według Ciebie wszystko jest średnie 

 Ciekawe jak zrobi Kacper..
Ciekawe jak zrobi Kacper.. 



 Co innego policzyć pole zawarte pomiędzy parabolą a jakąś wykresem jakieś funkcji.
I właśnie pokazałeś, że nie wiesz co to jest całka i do czego służy
Co innego policzyć pole zawarte pomiędzy parabolą a jakąś wykresem jakieś funkcji.
I właśnie pokazałeś, że nie wiesz co to jest całka i do czego służy  K.O
K.O

 mam na mysli takie cos (pole zaznaczone czerwonymi kreskami)...
zawsze mam tak, ze moje slowa nie wyrazaja tego co mysle ; )
mam na mysli takie cos (pole zaznaczone czerwonymi kreskami)...
zawsze mam tak, ze moje slowa nie wyrazaja tego co mysle ; )




 chociaz jedno udowodnie !
chociaz jedno udowodnie !




 |PB| = √a2+b2
|RQ| = √a2+b2
|PB| = √a2+b2
|RQ| = √a2+b2












 : D
: D
 Rozwiąż równanie:
Rozwiąż równanie:

 W między czasie odrzuciliśmy a = 0, a to jest z pewnością rozwiązaniem
W między czasie odrzuciliśmy a = 0, a to jest z pewnością rozwiązaniem 



 )
)

 (Jadę na zakupy i rozwiązania podam jak wrócę)
Benny − nie miałem nierówności Cauchy'ego w LO, ale na studiach pisałem magisterkę o tym
(Jadę na zakupy i rozwiązania podam jak wrócę)
Benny − nie miałem nierówności Cauchy'ego w LO, ale na studiach pisałem magisterkę o tym
 Poza tym zadanie z logarytmem nie pójdzie bez znajomości pewnego twierdzenia.
Znam książkę, z której to zadanie wzięto. Zapewne autor sam nie umie go rozwiązać, ale na
szczęście tam jest pełne rozwiązanie
Poza tym zadanie z logarytmem nie pójdzie bez znajomości pewnego twierdzenia.
Znam książkę, z której to zadanie wzięto. Zapewne autor sam nie umie go rozwiązać, ale na
szczęście tam jest pełne rozwiązanie 
 Dostałem 2n(2n+1)/(n+1)=x(2n+1)/(n+1) chyba, że sobie spierwiastkuje i dostanę x=2n lub
jest błąd i x=2
Dostałem 2n(2n+1)/(n+1)=x(2n+1)/(n+1) chyba, że sobie spierwiastkuje i dostanę x=2n lub
jest błąd i x=2 



 to jest typowy ciąg nietypowy
ahahah, zapomnialem dodac jeden na koncu , faktycznie tam lekko skopalem
a co do tego ciagu
to jest typowy ciąg nietypowy
ahahah, zapomnialem dodac jeden na koncu , faktycznie tam lekko skopalem
a co do tego ciagu


 ? Pisałem to w nocy
? Pisałem to w nocy 




 jakby nie było widać ..bo się chyba pogubiłam o co kto pytał
jakby nie było widać ..bo się chyba pogubiłam o co kto pytał 
 tak to jest jak post ma kilka
wątków
tak to jest jak post ma kilka
wątków 










 rzeczywiście uproszczona wersja
rzeczywiście uproszczona wersja 

