 mógłby ktoś mi podpowiedzieć
mógłby ktoś mi podpowiedzieć
 Jeżeli uczyłeś się o kręgach wpisanych w wielokąty to na pewno był wzór
na pole Δ w zależności od r.
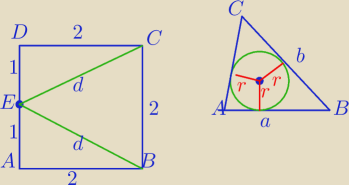
Promienie są prostopadłe do boków Δ w punktach styczności:
Jeżeli uczyłeś się o kręgach wpisanych w wielokąty to na pewno był wzór
na pole Δ w zależności od r.
Promienie są prostopadłe do boków Δ w punktach styczności:
| 1 | 1 | 1 | ||||
PΔABC= | *a*r+ | *b*r+ | *c*r⇔ | |||
| 2 | 2 | 2 |
| a+b+c | ||
PΔABC= | *r −p− połowa obwodu trójkąta pomnożona przez r . | |
| 2 |
| 1+2+√5 | ||
PΔ= | *r | |
| 2 |
| 1 | 1+2+√5 | ||
*1*2= | *r⇔ | ||
| 2 | 2 |
| 3−√5 | ||
r= | ||
| 2 |
| 2+√5+√5 | ||
p= | − połowa obwodu Δ | |
| 2 |
| 1 | ||
PΔBCE= | *2*2=2 | |
| 2 |
| 2 | ||
r'= | ||
| 1+√5 |
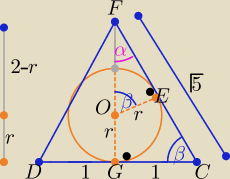 Z podobieństwa trójkątów GCF i OEF z cechy (kkk)
Z podobieństwa trójkątów GCF i OEF z cechy (kkk)
| 1 | r | |||
= | ⇒ r=........... | |||
| √5 | 2−r |
 ten pierwszy promień też mam taki, tylko troche inaczej liczyłem
1.pitagoras.
2.potem na dole wyszedł kwadrat r na r z promieni
3.boki styczne porównałem i wszytsko równaniem do obwodu trójkąta
ale mam problem z tym środkowym trójkatem równoramiennym, jestem w gimnazjum i nie mamy takich
wzorów, wiem o nim bo patrzyłem na te zadania, stad pytam czy da sie to zrobić bez użycia tych
wzorów ?
ten pierwszy promień też mam taki, tylko troche inaczej liczyłem
1.pitagoras.
2.potem na dole wyszedł kwadrat r na r z promieni
3.boki styczne porównałem i wszytsko równaniem do obwodu trójkąta
ale mam problem z tym środkowym trójkatem równoramiennym, jestem w gimnazjum i nie mamy takich
wzorów, wiem o nim bo patrzyłem na te zadania, stad pytam czy da sie to zrobić bez użycia tych
wzorów ?
 tak podobieństwo miałem i nie widziałem tego, ale teraz stokrotne dzięki
tak podobieństwo miałem i nie widziałem tego, ale teraz stokrotne dzięki 
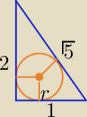
| a+b−c | ||
r= | ||
| 2 |
| 2+1−√5 | 3−√5 | |||
r= | = | |||
| 2 | 2 |
| 1 | ||
PΔ= | *2*2= 2 | |
| 2 |
| 2P | 4 | 2 | ||||
r= | ⇒ r= | = | ||||
| 2+√5+√5 | 2(1+√5) | 1+√5 |
 dzięki
dzięki
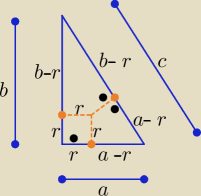 Dla każdego trójkąta prostokątnego:
Dla każdego trójkąta prostokątnego:
| a+b−c | ||
c= a−r+b−r ⇒ 2r=a+b −c ⇒ r= | ||
| 2 |
 ale ja nie mogę od razu napisać r=(a+b−c):2 i sobie podstawić, tylko stycznymi i
zwykłym równaniem choć wiem, że to zrobiłem
ale ja nie mogę od razu napisać r=(a+b−c):2 i sobie podstawić, tylko stycznymi i
zwykłym równaniem choć wiem, że to zrobiłem  , ale nie uznają mi jeśli tak od razu napiszę
, ale nie uznają mi jeśli tak od razu napiszę
