Zadanie z próbnej matury rozszerzonej - wykaż Indygo: http://zapodaj.net/6fcad4ca2eca8.jpg.html Mam takie zadanie z próbnej matury do rozwiązania na jutro. Mój matematyk powiedział, że cały dzień mu ono zajęło i gdyby on pisał taką maturę to po prostu by je pominął, a ja mam je zrobić w jedno popołudnie.... Dlatego proszę Was o pomoc, nawet najmniejszą wskazówkę. Nie mam żadnego pomysłu jak do tego podejść.

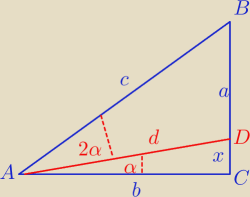
Janek191: Próbuj : 1) a² = d² + c² − 2 c d cos 2α x² = d² + b² − 2 b d cos α ( a + x)² = b² + c² − 2 b c cos 3α b² + ( a + x)² = c² 2) P = 0,5 (a + x)*b P = 0,5 b*d sin α + 0,5 c*d sin 2α c² = b² + (a + x)²

b
	= cos α
d

Jack: było... https://matematykaszkolna.pl/forum/312460.html

piotr1973: b=AC p=AB x=CD s=AD 1) sin(α)=x/s 2) sin(3α)=(x+a)/p 3) cos(α)=b/s 4) cos(3α)=b/p wyznaczyć z 4) b i wstawić do 3) potem z tego wyznaczyć p i wstawić do 2) z 1) wyznaczyć x i wstawić do 2) otrzymamy równanie z a, α, i niewiadomą s czyli AD wyznaczyć s i wyjdzie

piotr1973: po przekształceniach: sin(3alfa)=(a+sin(alfa)*s)/(cos(alfa)*s/cos(3alfa))

piotr1973:

	a+sin(α) s
sin(3α) =
	s   cos(α)   cos(3α)

stąd wyznaczyć s

Indygo: Wielkie dzięki!