Wyznacz ekstrema lokalne:
extremalna: Wyznacz ekstrema lokalne:
f(x)=(x−4)3(2x−1)4
Z góry dzięki
13 sty 17:03
13 sty 17:11
zzz: G(f(x))`=g`(x)*f(x)+g(x)*f`(x)
Jerzy z tego trzeba skorzystać ?
13 sty 17:12
Jerzy:
tak najprościej ..tylko to jest wzór na: [f(x)*g(x)]'
13 sty 17:16
zzz: Oks spróbuję policzyć ciekawe czy coś z tego wyjdzie
13 sty 17:17
zzz: ((x−4)
3)`*(2x−1)
4+(x−4)
3*((2x−1)
4)`
(x
3−3x
2*4+3x*16−64)`(2x−1)
4+(x−4)
3*(16x
4−24x
3+12x
2−8x+1)`
(x
3−12x
2+48x−64)`(2x−1)
4+(x−4)
3*(16x
4−24x
3+12x
2−8x+1)`
(3x
2−24x+48)(2x−1)
4+(x−4)
3*(64x
3−72x
2+24x−8)
(3x
2−24x+48)(16x
4−24x
3+12x
2−8x+1)+(x
3−3x
2*4+3x*16−64)(64x
3−72x
2+24x−8)
...
Nie da się łatwiej ?
13 sty 17:29
Jerzy:
musieli "podpaść " asystentowi
13 sty 17:30
zzz: A to co liczę jest dobrze ?
13 sty 17:30
extremalna: Da się łatwiej czy sie nie da? Bo liczę podobnie jak zzz.
13 sty 17:31
Jerzy:
f'(x) = 3(x−4)2(2x−1)4 + (x−4)3*4(2x−1)3 .. i teraz coś kombinuj
13 sty 17:31
Jerzy:
jeszcze drugi człon pomnożyć przez 2
13 sty 17:33
Jerzy:
wyłączcie: (2x−1)3(x−4)2 przed nawias
13 sty 17:34
zzz: (48x
6−72x
5+36x
4−24x
3+3x
2−384x
5+576x
4−288x
3+192x
2−24x+768x
4−1152x
3
+576x
2−384x+48)+(64x
6−72x
5+24x
4−8x
3−768x
5+864x
4−288x
3+96x
2+3072x
4−
3456x
3+1152x
2−384x−4096x
3+4608x
2−1536x+512)
No to pora na redukcję
13 sty 17:39
Jerzy:
zarąbiesz się ... patrz post 17:31 , a potem 17:34 ... i prościutko masz postać iloczynową
13 sty 17:41
extremalna:
13 sty 17:42
extremalna: licz licz...
13 sty 17:42
zzz: 112x
6−1296x
5+5340x
4−9312x
3+6627x
2−2328x+560
Koniec
13 sty 17:44
extremalna: No to teraz do 0 i ekstrema. Ja licze sposobem Jerzego.
13 sty 17:44
Jerzy:
i co Ci z tego przyszło .. teraz trzeba szukac miejsc zerowych tej pochodnej
13 sty 17:44
Jerzy:
przecież najprościej wyznaczycie miejsca zerowe z postaci iloczynowej
13 sty 17:45
zzz: Wziąłeś pochodną z (x−4)3 i (2x−1)4 ?
13 sty 17:45
extremalna: Ale pochodną i tak trzeba liczyć?
13 sty 17:46
Jerzy:
przecież to jest własnie pochodna
13 sty 17:46
Jerzy:
policzyłem pochodną iloczynu .. patrz 17:31
13 sty 17:47
Jerzy:
przeanalizujcie , po wyłaczeniu... dostajecie: f'(x) = (2x−1)3(x−4)2*[(3(2x−1) + 8(x−4)]
i tylko uporzadkowac nawias kwadratowy
13 sty 17:51
Jerzy:
z postaci 17:31 wyłaczyłem przed nawias 17:34
13 sty 17:52
zzz: Cholera jakoś nie łapię co ty tam zrobiłeś
13 sty 17:59
zzz:
13 sty 18:34
extremalna:
| | 1 | |
Wyszlo mi x=− |
| v x=4 v x=1,9 |
| | 2 | |
Czy dobrze?
13 sty 22:21
Włodek: Obawiam się że nie.
13 sty 22:33
monootonoczny: Co robie źle
Z pochodnej wychodzi (2x−1)
3(x−4
2)(10x−19)=0 ?
13 sty 22:54
zzz: x=16
v
x=1,9
v
x=0,5
13 sty 22:59
Włodek: (14x−35)(x−4)2(2x−1)3
13 sty 23:17
Qulka: 1/2 5/2 4
13 sty 23:19
monootonoczny: Więc kto ma dobrze? zzz czy Qulka?
13 sty 23:42
Qulka: podstaw sobie pod x i sprawdź kiedy masz w wyniku zero
13 sty 23:50
Qulka:
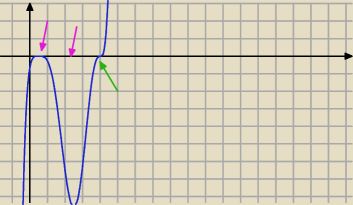
ekstremum w 1/2 i 5/2 ... w 4 pp
14 sty 00:15
monootonoczny: Dzięki
14 sty 00:17