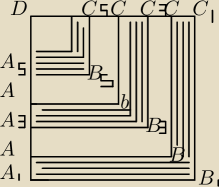
Nieskończony ciąg geometryczny rojo: Na rysunku przedstawiono fragment nieskończonego ciągu na przemian czarnych i białych kwadratów o wspólnym wierzchołku D. Kwadrat A1B1C1D koloru czarnego ma bok długości 3√13. Długość boku każdego następnego kwadratu stanowi 2/3 długości boku kwadratu poprzedniego. Oblicz pole obszaru zaznaczonego kolorem czarnym w nieskończonym ciągu tych kwadratów.

Qulka: a²−(2/3)²a²+(2/3)⁴a² − (2/3)⁶a² + ....... =9/5 •a² = 9/5 • 9•13

Kacper: Napiszę do szkoły żebyś dostał 0 procent.

Kacper: Życzę powodzenia na prawdziwej maturze.

abel: co to za matura pisana o 1:51 w nocy?

Kacper: Zdziwiłbyś/aś się

Ania: skąd się wzięło 9/5?

Ludwik Montgomery: no właśnie, ciekawe pytanie: skąd się wzięło 9/5?

Ludwik Montgomery: już wiem natchnęła mnie poezja Mickiewicza

Ania: oświec mnie, bo ja tak patrzę i nadal nie wiem

Qulka: stąd https://matematykaszkolna.pl/strona/297.html

Ania: Właśnie ja liczyłam q i mi wyszło −(2/3)², ale może gdzieś błąd popełniłam głupi

piotr1973: ∑_n=0^∞ a²(−1)ⁿ (2/3)²ⁿ = 9/13a²

piotr1973:

	a1		a2
wzór		=
	1−q		4   1+   9

Kacper: Wynik to 81